Задание №1871
Исследуйте отражение звука. Для этого возьмите двух− или трёхлитровый бидон и на дно положите механические часы (рис. 285, а). Поставьте бидон так, чтобы ухо было ниже его отверстия и не был слышен звук часов. Используя кусок фанеры (или плотного картона) и держа её так, как показано на рисунке 285, б, добейтесь отчётливого звучания часов. Сделайте вывод.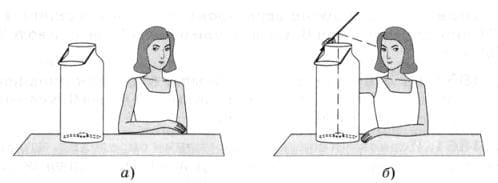 рис. 285
рис. 285
Решение
Оборудование:
Двух− или трёхлитровый бидон, механические часы, кусок фанеры (плотного картона).
Ход работы:
1. На дно бидона положите механические часы.
2. Поставьте бидон так, чтобы ухо было ниже его отверстия и не был слышен звук часов.
3. Поворачивая фанеру (картон), добейтесь отчётливого звучания часов.
Вывод:
Опыт и наблюдения показывают, что звуковая волна, так же как и механическая, отражается от препятствий. Отражение звука подчинено определенному закону: угол падения равен углу отражения.
Задание №1872
Проведите опыт по проверке наличия трещин в фарфоровой посуде. Объясните опыт.
Решение
Оборудование:
Фарфоровые чашки с трещиной и без трещины, карандаш.
Ход работы:
1. Постучим карандашом по краю фарфоровой чашки без трещины. Прислушайтесь к издаваемому звуку.
2. Постучим карандашом по краю фарфоровой чашки с трещиной. Прислушайтесь к издаваемому звуку.
Вывод:
Если фарфоровая чашка целая, звук от удара карандаша будет резонировать внутри посудины и услышим звон. Если в стенке чашки будет трещина, то этого не произойдет, звук будет глухим.
Задание №1873
Два динамика (рис. 286) подключены к выходу одного генератора электрических колебаний и излучают звуковые волны. На рисунке показаны сплошные линии, соответствующие максимальной плотности воздуха при распространении звука от каждого из динамиков, и штриховые линии, соответствующие минимальной плотности. В какой из точек 1 − 4 практически не слышно звука?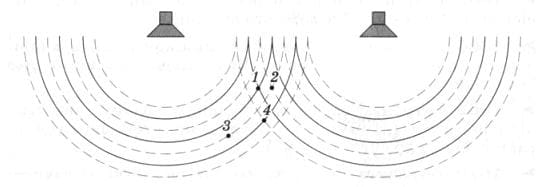 рис. 286
рис. 286
Решение
В точке 4. в точке 4 минимальное и максимальное давление складывается и получается ноль
Задание №1874
Имеются два когерентных источника звука, совершающих колебания в одинаковых фазах. В точке, отстоящей от первого источника на $x_{1} = 2,3$ м и от второго на $x_{2} = 2,48$ м, звук не слышен. Минимальная частота, при которой это возможно, ν = 1 кГц. Найдите скорость звука.
Решение
Дано:
$x_{1} = 2,3$ м;
$x_{2} = 2,48$ м;
ν = 1 кГц.
Найти:
v − ?
СИ:
ν = 1 000 Гц.
Решение:
Найдем разность хода двух звуковых волн:
$△x = x_{2} - x_{1}$ (м);
Звук не будет слышан, если звуковые волны от источников в заданной точке окажутся в противофазе, т. е. смещение составит половину длины волны:
$△x = \frac{λ }{2} = x_{2} - x_{1}$;
$λ = 2 * (x_{2} - x_{1})$;
Найдем скорость распространения звуковых колебаний:
$v = νλ = 2ν * (x_{2} - x_{1})$;
v = 2 * 1000 * (2,48 − 2,3) = 360 м/с.
Ответ: 360 м/с.

