Задание №1415

Рассмотрите графики движения двух тел (рис. 226) и ответьте на следующие вопросы:
а) Каковы виды этих движений?
б) Чем они различаются?
в) Чему равны скорости движения этих тел?
г) Чему равен путь, пройденный каждым телом за 10 с?
По рисунку определите время и место встречи этих тел.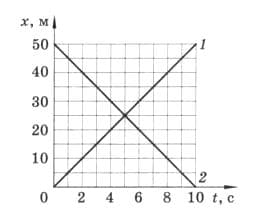
рис. 226

Решение

а) Равномерное прямолинейное движение.
б) Тела движутся навстречу друг другу, скорости движения тел направлены противоположно друг другу.
в) $x_{o}(1) = 0$ м; x (1) = 50 м;
$x_{o}(2) = 50$ м; x (2) = 0 м;
Для равномерного прямолинейного движения уравнение координаты:
$x = x_{o} + v_{x}t$;
$x - x_{o} = v_{x}t$;
$v_{x} = \frac{x - x_{o}}{t}$;
$v_{x1} = \frac{50 - 0}{10} = 5 $ м/с;
$v_{x2} = \frac{0 - 50}{10} = -5$ м/с.
г) $S_{1} = 5 * 10 = 50$ м;
$S_{2} = 5 * 10 = 50$ м.
По графику определим время и место встречи двух тел.
t = 5 c.; s = 25 м от начала движения каждого тела.

Задание №1416

На рисунке 227 изображены графики движения двух тел. Определите:
а) виды этих движений;
б) чем они различаются;
в) чему равны скорости движения этих тел;
г) чему равен путь, пройденный каждым телом за 6 с.
По рисунку определите время и место встречи этих тел.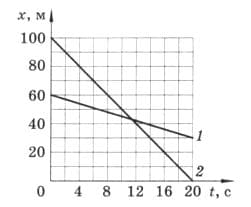
рис. 227

Решение

а) Равномерное прямолинейное движение.
б) Графики различаются скоростью движения тел (разный тангенс угла наклона графика к оси времени), координатой начала движения.
в) $x_{o(1)} = 60$ м; $x_{1} = 30$ м;
$x_{o(2)}= 100$ м; $x_{2} = 0$ м;
Для равномерного прямолинейного движения уравнение координаты:
$x = x_{o} + v_{x}t$;
$x - x_{o} = v_{x}t$;
$v_{x} = \frac{x - x_{o}}{t}$;
$v_{x1} = \frac{30 - 60}{20} = -1,5$ м/с;
$v_{x2} = \frac{0 - 100}{20} = -5 $ м/с.
г) $S_{1} = v_{1}t = 1,5 * 6 = 9$ м;
$S_{2} = v_{2}t = 5 * 6 = 30$ м.
д) По графику определим время и место встречи двух тел.
t ≈ 11 c.; s ≈ 17 м от начала движения 1−го тела.

Задание №1417

Любознательный Артём отправился в путешествие. При этом он двигался разными способами: на мотоцикле, пешком, на велосипеде и далее на вертолёте. Пользуясь графиком (рис. 228), ответьте на следующие вопросы:
а) Где оказался Артём через 2 ч после начала движения?
б) Каким видом транспорта предположительно он двигался на каждом участке пути?
в) Сколько времени и когда он отдыхал?
г) Сколько всего времени Артём был в пути?
Составьте самостоятельно задачу о своём движении из школы домой. Постройте примерный график этого движения.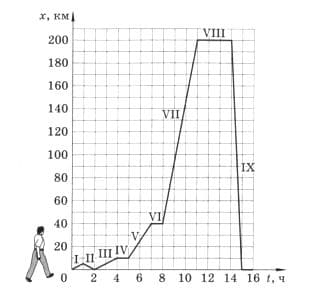
рис. 228

Решение

а) Артём через 2 ч после начала движения вернулся домой.
б) На участках пути I,II, III Артём двигался пешком, на участке V − на велосипеде, на участке VII − на мотоцикле, на участке IX − на вертолёте.
в) Артём отдыхал 1 час на IV участке пути, 1 час на VI участке пути, 3 часа на VIII участке пути. Всего 5 часов через 4, 7, 11 ч. пути.
г) После второго выхода из дома Артём был в пути 13 ч.
Задача.
Ученик вышел из дома и через 2 минуты после начала движения остановился проверить все ли учебники в портфеле. Затем по пути зашел в магазин. Остаток пути ученик бежал в школу.
Какой путь проделал ученик? (Ответ: 600 м).
Сколько всего времени ученик был в пути? (Ответ: 11 мин.).
Сколько времени ученик шел пешком? (Ответ: 5 мин.).
Сколько времени ученик бежал? (Ответ: 3 мин.).
Через сколько метров от дома находится магазин? (Ответ: 250 м).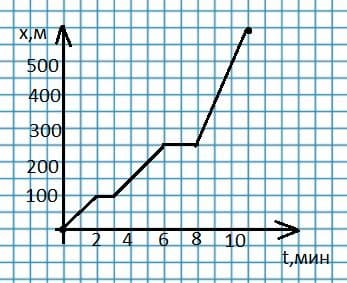

Задание №1418

В безветренную погоду капли дождя оставили на окне равномерно движущегося трамвая следы, направленные под углом 45° к вертикали. Найдите скорость трамвая, если скорость падения капель относительно Земли 36 км/ч.

Решение

Дано:
α = 45°;
$v_{к} = 36$ км/ч.
Найти:
$v_{тр}$ − ?
СИ:
$v_{к} = 10$ м/с.
Решение: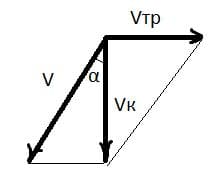
По закону сложения скоростей:
$v_{к} = v + v_{тр}$;
$tgα = \frac{v_{тр}}{v_{к}}$;
$v_{тр} = tgα * v_{к}$;
$v_{тр} = tg45° * 10 = 10$ м/с.
Ответ: 10 м/с.

Задание №1419

Гребец переправляется на лодке через реку шириной 400 м, удерживая всё время лодку перпендикулярно волнам. Скорость лодки относительно воды 6 км/ч, скорость течения реки 3 км/ч. Сколько времени займёт переправа? На сколько снесёт лодку вниз по течению реки за время переправы? Сколько времени заняла бы эта переправа в неподвижной воде?

Решение

Дано:
S = 400 м;
$v_{л} = 6$ км/ч;
$v_{р} = 3$ км/ч.
Найти:
t − ?
$t_{неподв}$ − ?
l − ?
СИ:
$v_{л} = 1,67$ м/с;
$v_{р} = 0,83$ м/с.
Решение: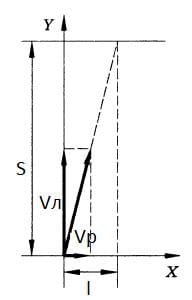
Найдем время переправы:
$S = v_{л}t$;
$t = \frac{S}{v_{л}}$;
$t = \frac{400}{1,67} = 240$ с;
$t = t_{неподв} = 240$ c.
Найдем расстояние, на которое снесет лодку:
$l = v_{р}t$;
l = 0,83 * 240 ≈ 200 м.
Ответ: 240 с; 240 с; 200 м.