Задание №1579

В начале подъёма в лифте высотного здания человек ощущает, что его прижимает к полу лифта. Изменяются ли при этом:
а) масса человека;
б) сила тяжести, действующая на человека;
в) вес человека?

Решение

а) Масса человека не изменяется.

б) Сила тяжести, действующая на тело, зависит от его массы и ускорения свободного падения. При подъёме лифта изменяется только ускорение, т.к. увеличивается расстояние до центра Земли, однако это изменение незначительно. Таким образом, сила тяжести уменьшается очень незначительно.

в) В начале подъёма лифт движется с ускорением, человек по инерции стремится остаться на месте, поэтому он начинает сильнее воздействовать на пол лифта, следовательно, его все увеличивается.

Задание №1580

На тросе висит груз. Укажите точки приложения веса груза и силы тяжести. Ответ поясните рисунком.

Решение

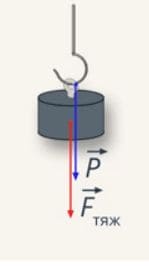Вес – это сила упругости, приложенная к подвесу со стороны тела, а сила тяжести – это сила, приложенная к телу со стороны Земли.

Задание №1581

Динамометр, на котором подвешен груз, начинает падать с некоторой высоты. Указатель динамометра при этом устанавливается на нуле. Можно ли сказать, что равны нулю:
а) вес груза;
б) масса груза;
в) сила тяжести?

Решение

а) Вес груза равен нулю. В данном случае и груз, и динамометр движутся с одинаковым ускорением, не оказывая друг на друга никакого влияния.

б) Масса груза не равна нулю.

в) Сила тяжести груза не равна нулю.

Задание №1582

Аквалангист, плавающий под водой, находится в состоянии равновесия при любом положении тела. Будет ли это состоянием невесомости?

Решение

Не будет, так как в теле не исчезают внутренние напряжения. Кроме того, оно оказывает давление на опору (воду).

Задание №1583

Мальчик, поднявшись на лестницу, случайно выронил ведро с водой. С какой силой давит вода на дно ведра во время падения?

Решение

С силой, равной нулю.

Задание №1584

Весы, на которых человек держит в руке тяжёлый груз, уравновешены. Что произойдёт с показаниями весов, если человек быстро поднимет груз?

Решение

В начале подъёма груза показания весов увеличатся, т.к. P = m * (g + a).

Задание №1585

С каким ускорением следует поднимать груз, чтобы его вес удвоился? С каким ускорением надо его опускать, чтобы вес уменьшился вдвое?

Решение

Дано:
$P_{2} = 2P_{1}$;
$P_{2} = \frac{P_{1}}{2}$.
Найти:
$a_{1}$ − ?
$a_{2}$ − ?
Решение:
Во время поднятия на груз действуют сила тяжести и сила реакции опоры. Согласно второму закону Ньютона:
$a_{1} = \frac{F}{m} = \frac{N - F_{т}}{m} = \frac{N - mg}{m} $;
$ma_{1} = N - mg$;
$N = ma_{1} + mg = m (a_{1} + g)$;
По третьему закону вес равен по модулю силе реакции опоры:
$N = P_{2} = m (a_{1} + g)$;
$P_{1} = mg$;
Ускорение гири при подъеме:
$P_{2} = 2P_{1}$;
$m (a_{1} + g) = 2 mg$;
$a_{1} + g = 2g$;
$a_{1} = 2g - g$
$a_{1} = g$;
Во время опускания на груз действуют сила тяжести и сила реакции опоры. Согласно второму закону Ньютона:
$a_{2} = \frac{F}{m} = \frac{N + F_{т}}{m} = \frac{N + mg}{m} $;
$ma_{2} = N + mg$;
$N = mg - ma_{2} = m (g -a_{2})$;
По третьему закону вес равен по модулю силе реакции опоры:
$N = P_{2} = m (g - a_{2})$;
Ускорение гири при опускании:
$P_{2} = \frac{P_{1}}{2}$;
$m (g - a_{2}) = \frac{mg}{2}$;
$g - a_{2} = \frac{g}{2}$;
$a_{2} = g - \frac{g}{2} = \frac{g}{2}$.
Ответ: g; $\frac{g}{2}$.

Задание №1586

Как измерить массу тела в условиях невесомости?

Решение

Согласно второму закону Ньютона имеем $m = \frac{F}{a}$. Следовательно, нужно измерить ускорение, сообщаемое телу силой, известной по модулю. Это может быть сила упругости пружины.

Задание №1587

Известно, что вес одного и того же тела на Луне примерно в 6 раз меньше, чем на Земле. Какого веса штангу смог бы поднять спортсмен на Луне, если на Земле он поднимает штангу весом 1000 Н? Какую массу будет иметь эта штанга?

Решение

Дано:
F = 1000 Н;
$g_{з} ≈ 10$ Н/кг.
Найти:
$P_{л}$ − ?
m − ?
Решение:
Чтобы поднять тело, необходимо приложить силу, равную силе тяжести, действующей на тело. Сила для поднятия обоих тел одинакова. По второму закону Ньютона:
F = P = mg;
$F = P_{з} = P_{л} = 1000$ Н;
Если на Луне штанга весит 1000 Н, то на Земле в 6 раз больше − 6000 Н.
Масса штанги равна:
$m = \frac{P_{з}}{g_{з}}$;
$m = \frac{6000}{10} = 600 кг$.
Ответ: 1000 Н; 600 кг.

Задание №1588

Космическая ракета при старте с поверхности Земли движется вертикально с ускорением 20 $м/с^{2}$. Чему равен вес лётчика−космонавта в кабине, если его масса 80 кг?

Решение

Дано:
$a = 20 м/с^{2}$;
m = 80 кг;
$g ≈ 10 м/с^{2}$.
Найти:
P − ?
Решение:
В ракете, движущейся с ускорением а, на космонавта действуют сила тяжести и сила реакции опоры. Согласно второму закону Ньютона:
$a = \frac{F}{m} = \frac{N - F_{т}}{m} = \frac{N - mg}{m} $;
ma = N − mg;
N = ma + mg = m (a + g);
По третьему закону вес космонавта равен по модулю силе реакции опоры:
N = P = m (a + g);
P = 80 * (20 + 10) = 2400 Н = 2,4 кН.
Ответ: 2,4 кН.

Задание №1589

Лифт, начинающий подниматься вверх, разгоняется до скорости 5 м/с в течение 10 с. Определите, чему будет равен при этом вес пассажира лифта массой 75 кг.

Решение

Дано:
v = 5 м/с;
t = 10 c;
m = 75 кг;
$g ≈ 10 м/с^{2}$.
Найти:
P − ?
Решение:
Уравнение скорости:
$v = v_{0} + at$;
$a= \frac{v – v_{0}}{t}$;
Т.к. лифт начинает движение, то $v_{0} = 0$;
$a= \frac{v}{t}$;
$a= \frac{5}{10} = 0,5 м/с^{2}$;
В лифте, движущейся с ускорением а, на пассажира действуют сила тяжести и сила реакции опоры. Согласно второму закону Ньютона:
$a = \frac{F}{m} = \frac{N - F_{т}}{m} = \frac{N - mg}{m} $;
ma = N − mg;
N = ma + mg = m (a + g);
По третьему закону вес пассажира равен по модулю силе реакции опоры:
N = P = m (a + g);
P = 75 * (0,5 + 10) = 787,5 Н.
Ответ: 787,5 Н.

Задание №1590

Чему равен вес космонавта массой 80 кг в стартующей ракете, если перегрузка, которую он испытывает, равна 4?

Решение

Дано:
m = 80 кг;
k = 4;
$g ≈ 10 м/с^{2}$.
Найти:
$P_{2}$ − ?
Решение:
Перегрузка определяются отношением измененного веса космонавта к его исходному весу:
$k = \frac{P_{2}}{P_{1}}$;
$P_{1} = mg$;
$P_{2} = kP_{1} = kmg$;
$P_{2} = 4 * 80 * 10 = 3200 Н = 3,2$ кН.
Ответ: 3,2 кН.

Задание №1591

Рассчитайте перегрузку, испытываемую космонавтом в ракете, если масса космонавта 85 кг, а его вес во время старта ракеты увеличился до 5,1 кН.

Решение

Дано:
m = 85 кг;
$P_{2} = 5,1$ кН;
$g ≈ 9,8 м/с^{2}$.
Найти:
k − ?
СИ:
$P_{2} = 5100$ Н.
Решение:
$P_{1}= mg$;
Перегрузка определяются отношением измененного веса космонавта к его исходному весу:
$k = \frac{P_{2}}{P_{1}} = \frac{P_{2}}{mg}$;
$k = \frac{ 5100}{85 * 10} = 6$.
Ответ: 6.