Задание № 1281
Можно ли наблюдать лунное затмение с любой точки на поверхности Земли? Ответ поясните чертежом.
Решение
Как видно из рисунка, лунное затмение наблюдают в той части Земли, куда в тень зашла Луна.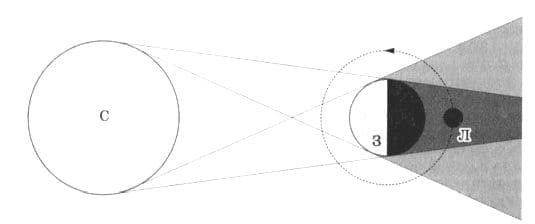
Задание № 1282
При каком условии непрозрачный предмет даёт тень без полутени?
Решение
Когда источник света точечный.
Задание № 1283
В каком случае от предмета получается только полутень?
Решение
Если источник света больше предмета, а экран должен находиться от предмета дальше, чем вершина конуса полной тени.
Задание № 1284
В какое время дня − утром, в полдень или вечером − размеры тени от облака на поверхности Земли наиболее близки к размерам самого облака? Ответ поясните с помощью чертежа.
Решение
В полдень.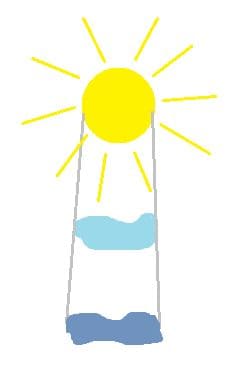
Задание № 1285
Что увидит космонавт, находясь на Луне, в то время как на Земле будет наблюдаться лунное затмение?
Решение
Космонавт, находясь на Луне, увидит солнечное затмение.
Задание № 1286
Объясните явление, описанное Н. В. Гоголем в "Повести о том, как поссорился Иван Иванович с Иваном Никифоровичем": "...Комната, в которую вступил Иван Иванович, была совершенно тёмной, потому что ставни были закрыты, и солнечный луч, проходя в дыру, сделанную в ставне... и ударяясь в противоположную стену, рисовал на ней пёстрый ландшафт из... крыш, дерев и развешанного на дворе платья, всё только в обращённом виде...".
Решение
Это объясняется прямолинейным распространением света через щель в ставне, создавался эффект перевёрнутой фотографии. Подобное устройство называется «камера−обскура».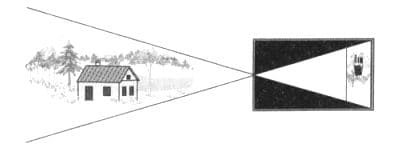
Задание № 1287
В солнечный день длина тени на земле от ёлки высотой 1,5 м равна 0,75 м, а от берёзы − 5 м. Чему равна высота берёзы?
Решение
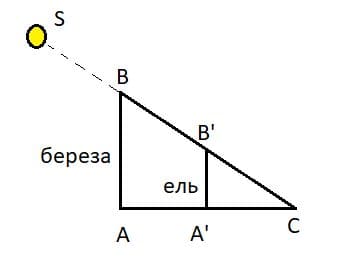 Дано:
Дано:
A'B' = 1,5 м;
A'C = 0,75 м;
AC = 5 м.
Найти:
AB − ?
Решение:
Деревья растут под углом 90° к поверхности Земли, расположим их на рисунке так, чтобы их тени заканчивались в одной точке С. Значит △A'B'C подобен △ABC, т.к. ∠CAB = ∠CA'B' = 90° и ∠C − общий.
$\frac{AB}{A'B'} = \frac{AC}{A'C}$;
$AB = \frac{A'B' * AC}{A'C}$;
$AB = \frac{1,5 * 5}{0,75} = 10$ м.
Ответ: 10 м.
Задание № 1288
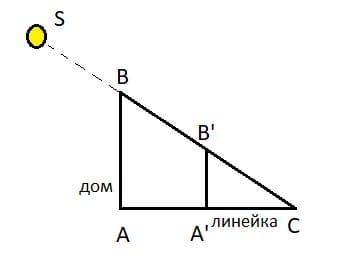
От отвесно поставленной метровой линейки в солнечную погоду длина тени равна 40 см. Определите высоту дома, если длина тени от него 4,8 м.
Решение
 Дано:
Дано:
A'B' = 1 м;
A'C = 40 см;
AC = 4,8 м.
Найти:
AB − ?
СИ:
A'C = 0,4 м.
Решение:
Расположим линейку и дерево на рисунке так, чтобы их тени заканчивались в одной точке С. Значит △A'B'C подобен △ABC, т.к. ∠CAB = ∠CA'B' = 90° и ∠C − общий.
$\frac{AB}{A'B'} = \frac{AC}{A'C}$;
$AB = \frac{A'B' * AC}{A'C}$;
$AB = \frac{1 * 4,8}{0,4} = 12$ м.
Ответ: 12 м.
Задание № 1289
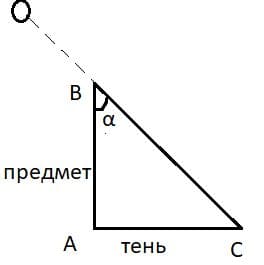
Чему равна угловая высота солнца над горизонтом, если длина тени от предмета равна его высоте?
Решение
 Дано:
Дано:
AB = AC.
Найти:
α − ?
Решение:
Если длина тени от предмета равна его высоте, то получается равнобедренный прямоугольный треугольник.
$tgα = \frac{AC}{AB} = 1$;
α = 45°.
Ответ: Угловая высота солнца над горизонтом равна 45°.
Задание № 1290
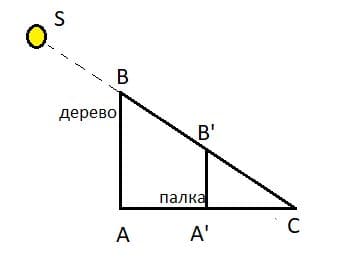
Палка длиной 1,2 м, поставленная вертикально, отбрасывает тень длиной 0,8 м. Длина тени от дерева в это же время оказалась в 12 раз больше длины палки. Чему равна высота дерева?
Решение
 Дано:
Дано:
A'B' = 1,2 м;
A'C = 0,8 м;
AC = 12A'B'.
Найти:
AB − ?
Решение:
Расположим палку и дерево на рисунке так, чтобы их тени заканчивались в одной точке С. Значит △A'B'C подобен △ABC, т.к. ∠CAB = ∠CA'B' = 90° и ∠C − общий.
$\frac{AB}{A'B'} = \frac{AC}{A'C}$;
$AB = \frac{A'B' * AC}{A'C} = \frac{A'B' * 12A'B'}{A'C}$;
$AB = \frac{1,2 * 12 * 1,2}{0,8} = 21,6$ м.
Ответ: 21,6 м.
Задание № 1291
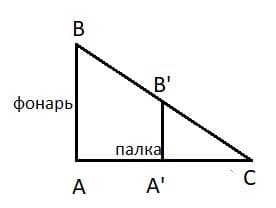
На высоте 4 м висит уличный фонарь. Рассчитайте длину тени, которую отбросит палка длиной 1 м, если её установить вертикально на расстоянии 3 м от основания столба, на котором укреплён фонарь.
Решение
 Дано:
Дано:
AB = 4 м;
A'B' = 1 м;
AA' = 3 м;
Найти:
A'C − ?
Решение:
Проведем луч от фонаря к верхней части палки. △A'B'C подобен △ABC, т.к. ∠CAB = ∠CA'B' = 90° и ∠C − общий.
AC = AA' +A'C;
$\frac{AB}{A'B'} = \frac{AC}{A'C} = \frac{ AA' +A'C}{A'C} $;
$\frac{4}{1} = \frac{3 + A'C }{A'C}$;
4A'C = 3 + A'C;
3A'C = 3;
A'C = 1 м.
Ответ: 1 м.
Задание № 1292
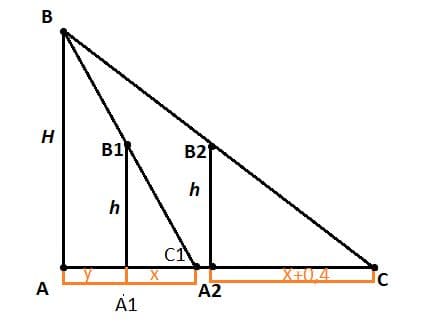
Два столбика одинаковой высоты 1,2 м поставлены вблизи уличного фонаря так, что расстояние от основания уличного фонаря до основания столбиков отличаются на 0,8 м. При этом тени, отбрасываемые столбиками, отличаются на 0,4 м. Найдите высоту, на которую подвешен фонарь.
Решение
 Дано:
Дано:
h = 1,2 м;
$AA_{2} - AA_{1} = 0,8$ м;
$A_{2}C- A_{1}C_{1} = 0,4$ м.
Найти:
H− ?
Решение:
△ABC подобен △$A_{2}B_{2}C$, т.к. $∠BAC = ∠B_{2}A_{2}C = 90°$ и ∠C − общий.
$A_{2}C = A_{1}C_{1} + 0,4$;
$AA_{2} - AA_{1} = A_{1}A_{2} = 0,8$ м;
$AC = AA_{1} + A_{1}A_{2} + A_{2}C = AA_{1} + 0,8 + A_{2}C$;
$\frac{H}{h} = \frac{AC}{A_{2}C} = \frac{AA_{1} + 0,8 + A_{2}C}{ A_{1}C_{1} + 0,4}$;
Пусть тень, отбрасываемая от первого столба ($A_{1}C_{1}$) равна x, тогда тень, отбрасываемая от второго столба ($A_{2}C$) равна (x + 0,4), расстояние от фонаря до столба ($AA_{1}$) равно y.
$\frac{H}{1,2} = \frac{y + 0,8 + x + 0,4}{x + 0,4} = \frac{y + x + 1,2}{x + 0,4}$;
△$ABC_{1}$ подобен △$A_{1}B_{1}C_{1}$, т.к. ∠$BAC_{1} = ∠B_{1}A_{1}C_{1} = 90°$ и ∠$C_{1}$ − общий.
$\frac{H}{h} = \frac{AC_{1}}{A_{1}C_{1}}$;
$AC_{1} = AA_{1} + A_{1}C_{1} = x + y$;
$\frac{H}{1,2} = \frac{x + y}{x}$;
$\begin{equation*} \begin{cases} \frac{H}{1,2} = \frac{х + y + 1,2}{x + 0,4} \\ \frac{H}{1,2} = \frac{x + y}{x} & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} H * (x + 0,4) = 1,2 * (x + y + 1,2) \\ Hx = 1,2 * (x + y) & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} Hx + 0,4x = 1,2 * (x + y) + 1,2 * 1,2 \\ Hx = 1,2 * (x + y); | * (-1) & \end{cases} \end{equation*}$
$\begin{equation*} \begin{cases} Hx + 0,4x = 1,2 * (x + y) + 1,44 \\ -Hx = -1,2 * (x + y); & \end{cases} \end{equation*}$
0,4x = 1,44;
$x = \frac{1,44}{0,4} = 3,6$ м.
Ответ: 3,6 м.

