Задание №589

К концу рычага приложены силы 8 и 40 Н. Длина рычага 90 см. Где находится точка опоры, если рычаг уравновешен?

Решение

Дано:
$F_{1} = 8$ Н;
$F_{2} = 40$ Н;
l = 90 см;
Найти:
О − ?
СИ:
l = 0,9 м.
Решение:
$\frac{F_{1}}{ F_{2}} = \frac{l_{2}}{ l_{1}} = \frac{l - l_{1}}{l_{1}}$;
$F_{1}l_{1} = F_{2} * (l - l_{1})$;
$F_{1}l_{1} + F_{2}l_{1} = F_{2}l$;
$l_{1} * (F_{1} + F_{2}) = F_{2}l$;
$l_{1} = \frac{F_{2}l}{F_{1} + F_{2}}$;
$l_{1} = \frac{40 * 0,9}{40 + 8} = 0,75$ м = 75 см.
Точка опоры находится на расстоянии 75 см от точки приложения меньшей силы.
Ответ: 75 см.

Задание №590

Определите меньшее плечо рычага, если при равновесии рычага на его большее плечо, равное 60 см, действует сила 40 Н, а на меньшее − 120 Н.

Решение

Дано:
$F_{1} = 120$ Н;
$F_{2} = 40$ Н;
$l_{2} = 60$ см;
Найти:
$l_{1}$ − ?
СИ:
$l_{2} = 0,6$ м;
Решение:
$\frac{F_{1}}{ F_{2}} = \frac{l_{2}}{ l_{1}}$;
$l_{1} = \frac{F_{2} * l_{2}}{F_{1}}$;
$l_{1} = \frac{40 * 0,6}{120} = 0,2$ м = 20 см.
Ответ: 20 см.

Задание №591

Чему равны силы $F_{1}$ и $F_{2}$, если рычаг находится в равновесии (рис. 87)?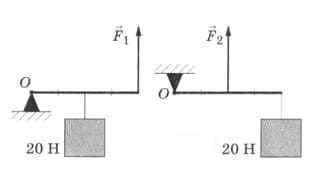
рис. 87

Решение

РИСУНОК 1
Дано:
F = 20 Н;
$\frac{l_{1}}{l} = 2$;
Найти:
$F_{1}$ − ?
Решение:
$\frac{F}{F_{1}} = \frac{l_{1}}{l} = 2$;
$F_{1} = \frac{F}{2}$;
$F_{1} = \frac{20}{2} = 10$ Н.
Ответ: 10 Н.

РИСУНОК 2
Дано:
F = 20 Н;
$\frac{l}{l_{2}} = 2$;
Найти:
$F_{2}$ − ?
Решение:
$\frac{F_{2}}{F} = \frac{l}{l_{2}} = 2$;
$F_{2} = 2F$;
$F_{1} = 2 * 20 = 40$ Н.
Ответ: 40 Н.

Задание №592

У рычага, находящегося в равновесии, плечи равны 30 и 40 см. К меньшему плечу приложена сила 120 Н. Какая сила приложена к большему плечу?

Решение

Дано:
$F_{1} = 120$ Н;
$l_{2} = 40$ см;
$l_{1} = 30$ см.
Найти:
$F_{2}$ − ?
СИ:
$l_{2} = 0,4$ м;
$l_{1} = 0,3$ м.
Решение:
$\frac{F_{1}}{F_{2}} = \frac{l_{2}}{l_{1}}$;
$F_{2} = \frac{F_{1}l_{1}}{l_{2}}$;
$F_{2} = \frac{120 * 0,3}{0,4} = 90$ Н.
Ответ: 90 Н.

Задание №593

Чему равна сила F, уравновешивающая груз массой 8 кг (рис. 88)?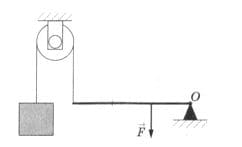
рис. 88

Решение

Дано:
$m_{1} = 8$ кг;
$\frac{l_{1}}{l} = 3$;
Найти:
F − ?
Решение:
F = mg;
$\frac{F}{F_{1}} = \frac{l_{1}}{l} = 3$;
$F = 3F_{1} = 3m_{1}g$;
g ≈10 Н/кг
$F = 3 * 8 * 10 = 240$ Н.
Ответ: 240 Н.

Задание №594

Каково назначение неподвижного блока, ведь он не даёт выигрыша в силе? Где его удобно использовать?

Решение

Неподвижный блок не даёт выигрыша в силе (F1 = F2), но позволяет изменять направление действия силы.
Примеры: жалюзи, подъёмный механизм башенного крана (используется система неподвижного и подвижного блоков, т. е. в соединении используются как натяжной блок), ворот в колодце, лебёдка, катушка спиннинга у рыбака.

Задание №595

Используя неподвижный блок, из воды поднимают гранитную плиту объёмом 0,03 $м^{3}$. Какую силу надо приложить, если плита находится в воде; на поверхности воды? Трение не учитывать.

Решение

Дано:
V = 0,03 $м^{3}$;
$ρ_{гр} = 2600 кг/м^{3}$;
$ρ_{в} = 1000 кг/м^{3}$.
Найти:
$F_{1}$ − ?
$F_{2}$ − ?
Решение:
Вес плиты в воздухе:
$P_{2} = mg = gρ_{гр}V$;
Сила Архимеда:
$F_{А} = gρ_{в}V$;
Вес плиты в воде:
$P_{1} = P_{2} - F_{А} = gρ_{гр}V - gρ_{в}V = gV * (ρ_{гр} - ρ_{в})$;
g ≈10 Н/кг;
Неподвижный блок не дает выигрыш в силе, значит:
$F_{1} = P_{1} = 10 * 0,03 * (2600 - 1000) = 480$ Н;
$F_{2} = P_{2} = 10 * 2600 * 0,03 = 780$ Н.
Ответ: 480 Н; 780 Н.

Задание №596

Рабочий поднимает на высоту 4 м груз весом 600 Н при помощи подвижного блока. С какой силой он тянет верёвку? Какой длины конец верёвки он при этом вытянет?

Решение

Дано:
$h_{1} = 4$ м;
P = 600 Н.
Найти:
F − ?
$h_{2}$ − ?
Решение:
Подвижный блок даёт выигрыш в силе в 2 раза.
$F=\frac{P}{2}$;
$F=\frac{600}{2} = 300$ Н;
Из "золотого правила механики" следует, что во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии.
$\frac{P}{F} = \frac{h_{2}}{h_{1}} = 2$;
$h_{2} = 2h_{1}$;
$h_{2} = 2 * 4 = 8$ м.
Ответ: 300 Н; 8 м.

Задание №597

При подъёме груза на высоту 3 м с помощью подвижного блока человек прикладывает к свободному концу верёвки силу 300 Н. Какую работу он при этом совершает?

Решение

Дано:
s = 3 м;
F = 300 Н.
Найти:
А − ?
Решение:
A = Ps, где P − сила, приложенная к грузу, s − высота, на которую поднят груз.
Подвижный блок даёт выигрыш в силе в 2 раза.
$F=\frac{P}{2}$;
P = 2F;
А = 2Fs;
А = 2 * 300 * 3 = 1800 Дж.
Ответ: 1800 Дж.

Задание №598

Рассчитайте КПД рычага, с помощью которого груз массой 245 кг равномерно подняли на высоту 6 см. При этом к большему плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см.

Решение

Дано:
$h_{1} = 30$ см;
$h_{2} = 6$ см;
m = 245 кг;
F = 500 Н.
Найти:
η − ?
СИ:
$h_{1} = 0,3$ м;
$h_{2} = 0,6$ м.
Решение:
$А_{п} = Fh_{2} = mgh_{2}$;
$А_{з} = Fh_{1}$;
$η =\frac{А_{п}}{А_{з}} * 100 = \frac{mgh_{2}}{Fh_{1}} * 100$ %;
g ≈10 Н/кг;
$η =\frac{245 * 10 * 0,6}{500 * 0,3} * 100 = 98$ %.
Ответ: 98 %.