Задание № 1328

Свеча расположена от плоского зеркала на расстоянии 20 см. На каком расстоянии от свечи находится её изображение? На каком расстоянии от свечи окажется изображение, если её отодвинуть от зеркала на 10 см?

Решение

Дано:
S = 20 см;
△S = 10 см.
Найти:
L − ?
$L_{1}$ − ?
Решение:
Мнимое изображение предмета в плоском зеркале находится на таком же расстоянии от зеркала, на каком находится сам предмет. Следовательно, расстояние между предметом и изображением равно двойному расстоянию от свечи до зеркала.
L = 2S;
L = 2 * 20 = 40 см;
$S_{1} = S - △S$;
$S_{1} = 20 - 10 = 10 $ см;
$L_{1} = 2S_{1}$;
$L_{1} = 2 * 10 = 20$ см.
Ответ: 20 см.

Задание № 1329

Расположите плоское зеркало так, чтобы катящийся по столу шарик казался в зеркале поднимающимся вертикально вверх. Объясните опыт.

Решение

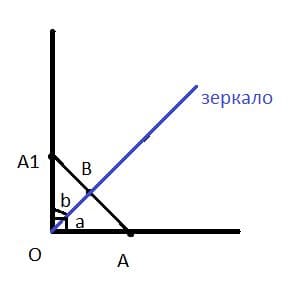Изобразим шарик А, движущийся по столу. Изображение шарика $A_{1}$ в зеркале находится в вертикальной плоскости. Выберем некоторую произвольную точку O в плоскости стола (точка O – это проекция на плоскость рисунка прямой, образованной при пересечении плоскости зеркала и плоскости стола). Покажем изображение шарика $A_{1}$ так, что $OA=OA_{1}$.
Далее соединяем точку A с $A_{1}$. Так как же изображение предмета в зеркале симметрично самому предмету относительно зеркала, то плоскость зеркала (необязательно само зеркало) проходит через середину отрезка $AA_{1}$ (точку B) и точку O.
Треугольники AOB и $A_{1}OB$ равны друг другу (по двум сторонам и углу между ними), поэтому углы AOB и $A_{1}OB$ равны друг другу. Значит:
a = b + b;
a = 2b;
$b = \frac{a}{2}$;
$b = \frac{90°}{2} = 45°$.
Ответ: Плоскость зеркала нужно расположить под углом 45 к плоскости стола.

Задание № 1330

Встаньте перед зеркалом и закройте ладонью левый глаз. Затем, не изменяя положения головы, пальцем, приложенным к зеркалу, закройте изображение левого глаза. После этого, закрыв правый глаз и открыв левый, пронаблюдайте, что закрытым окажется изображение не левого, а правого глаза. Объясните наблюдаемое явление.

Решение

Причина наблюдаемого явления − обратимость световых лучей: падающий и отраженный лучи меняются местами.

Задание № 1331

Чтобы видеть своё изображение во весь рост в плоском вертикальном зеркале, высота зеркала должна быть не меньше половины роста человека. Докажите это.

Решение

Способ 1.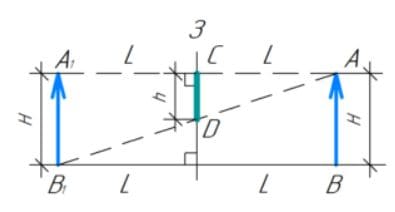
Изобразим человека в виде отрезка AB высотой H. Зеркало расположим на расстоянии L от человека. Известно, что изображение предмета в плоском зеркале симметрично самому предмету относительно плоскости зеркала. Поэтому для построения изображения человека в плоском зеркале построим точки $A_{1}$ и $B_{1}$, симметричные точкам A и B человека.
Из полученного рисунка видно, что для рассмотрения себя в полный рост человеку достаточно зеркала CD высотой h (человек видит изображение головы $A_{1}$ и стопы $B_{1})$.
Треугольники ACD и $AA_{1}B_{1}$ подобны по трем углам, поэтому:
$\frac{H}{h} = \frac{2L}{L}$;
$h = \frac{H}{2}$.
Таким образом, чтобы видеть своё изображение во весь рост в плоском вертикальном зеркале, высота зеркала должна быть не меньше половины роста человека.
Способ 2.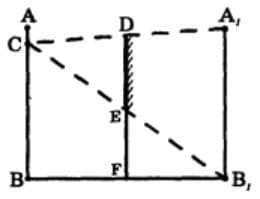
Изобразим человека в виде отрезка AB высотой H. Известно, что изображение предмета в плоском зеркале симметрично самому предмету относительно плоскости зеркала. Поэтому для построения изображения человека в плоском зеркале построим точки $A_{1}$ и $B_{1}$, симметричные точкам А и В человека. Точка С расположена на уровне глаз человека. DE − средняя линия △$CA_{1}B_{1}$.
$DE = \frac{A_{1}B_{1}}{2} = \frac{H}{2}$.
Таким образом, чтобы видеть своё изображение во весь рост в плоском вертикальном зеркале, высота зеркала должна быть не меньше половины роста человека.

Задание № 1332

На плоское зеркало, лежащее на столе, поставьте шахматную фигуру. Направьте на фигуру пучок света под небольшим углом так, чтобы на стене (экране) получить двойную тень фигуры − прямую и перевёрнутую. Построением покажите, почему это возможно.

Решение

Шахматная фигура AB загораживает падающий поток между лучами CC' и отраженный поток между лучами CC". В результате на экране появляется двойная тень − прямая B'A' и перевернутая A'B'.

Задание № 1333

Предложите способ определения высоты дерева, зная свой рост и размер обуви и имея лишь карманное зеркало.

Решение

Оборудование: карманное зеркало, полоска бумаги равная размеру обуви, данные о росте.
Ход работы:
1. Положим зеркало на некотором расстоянии от дерева.
2. Отойдем от зеркала, пока в нем не покажется крайняя верхняя точка дерева.
3. Измерим расстояние от точки себя до зеркала.
4. Измерим расстояние от зеркала до дерева.
5. Зная свой рост и пользуясь свойством подобных треугольников вычислим высоту дерева.
Объяснение:
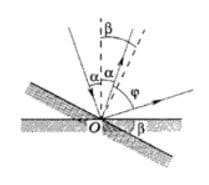
∠BDA − угол падения, ∠FDE − угол отражения;
∠BDA = ∠FDE;
∠BAD и DEF − прямые углы;
∠BAD = DEF.
△ABD и △DFE подобны по двум углам, значит стороны △DFE больше сторон △ABD в одно и то же число.
Таким образом, измеряемое дерево будет во столько раз выше нас, во сколько расстояние от него до зеркала больше расстояния от зеркала до вас.
$\frac{EF}{AB} = \frac{DE}{AD}$;
$EF = \frac{AB * DE}{AD}$.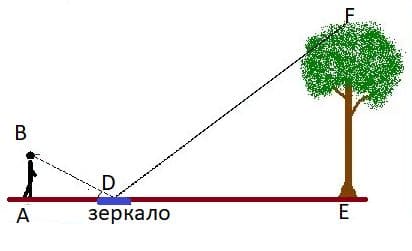

Задание № 1334

Положите на дно чашки монету и расположите глаз так, чтобы край чашки загораживал монету (рис. 208). Не изменяя положения глаза, наполните чашку водой. Почему монету стало видно?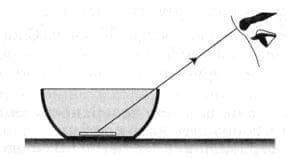
рис. 208

Решение

Так как лучи преломляются на границе сред воздух − вода, то глаз видит
монету в точке А.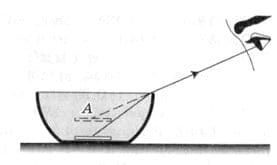

Задание № 1335

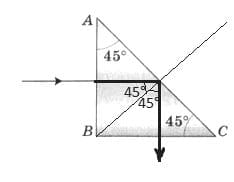
Луч направлен из воздуха на поверхность стеклянной призмы (рис. 209). Докажите, что выходящий из призмы луч направлен перпендикулярно грани ВС.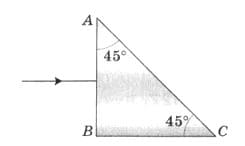
рис. 209

Решение

Т.к. луч падает перпендикулярно поверхности, то на входе преломления не происходит. Для стекла предельный угол полного внутреннего отражения равен 42°, поэтому луч, падая на грань призмы (гипотенузу треугольника АВС) под углом 45°, не выйдет из неё, а отразится под тем же углом. Поэтому на этой грани свет испытывает полное отражение. Это поворотная призма. Она поворачивает луч на 90°.