Задание №1553

Мяч, брошенный горизонтально с высоты 4 м над землёй, упал на расстоянии 12 м от места бросания. Найдите начальную и конечную скорости мяча.

Решение

Дано:
h = 4 м;
l = 12 м;
g ≈ 10 $м/с^{2}$.
Найти:
$v_{0}$ − ?
v − ?
Решение: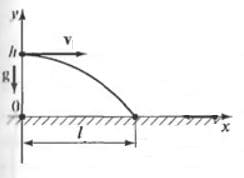
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = 0$; $g_{y} = g$; y = h; $y_{0} = 0$, то
$h =\frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
$v_{y} = gt = g * \sqrt{\frac{2h}{g}}$;
$v_{y} = 10 * \sqrt{\frac{2 * 4}{10}} = 8,9$ м/с;
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}$; x = l, то:
$l = v_{0}t$;
$v_{0} = \frac{l}{t} = \frac{l}{\sqrt{\frac{2d}{g}}} = {l}{\sqrt{\frac{g}{2d}}}$;
$v_{0} = 12{\sqrt{\frac{10}{2 * 4}}} = 13,4$ м/с;
Найдем конечную скорость по теореме Пифагора:
$V^{2} = V_{y}^{2} + V_{0}^{2}$;
$V = \sqrt{V_{y}^{2} + V_{0}^{2}}$;
$V = \sqrt{8,9^{2} + 13,4^{2}} = 16$ м/с.
Ответ: 16 м/с.

Задание №1554

Пуля вылетает в горизонтальном направлении и летит со средней скоростью 800 м/с. На сколько снизится пуля в вертикальном направлении во время полёта, если расстояние до цели 600 м?

Решение

Дано:
v = 800 м/с;
l = 600 м;
g ≈ 10 $м/с^{2}$.
Найти:
h − ?
Решение:
За начало отсчета координат примем точку, откуда вылетает пуля, а за начало отсчета времени − момент сбрасывания. Ось Ox направим горизонтально, а ось Oy − вертикально вверх. Движение можно представить как совокупность двух видов движения: равномерного, происходящего в горизонтальном направлении по инерции, и равноускоренного, происходящего в вертикальном направлении под действием силы тяжести.
Движение пули описывается уравнениями:
$x = v_{0}t cos α$;
$y = v_{0}t sin α + \frac{gt^{2}}{2}$;
Через время t пуля преодолеет расстояние:
$l = v_{0}t cos α$;
$t = \frac{l}{v_{0} cos α} = \frac{600}{800 * 1} = 0,75$ с;
Подставим время t в уравнение, получим расстояние, на которое снизится пули в отвесном направлении;
$h = 800 * 0,75 * sin 0 + \frac{10 * 0,75^{2}}{2} = 2,8$ м.
Ответ: 2,8 м.

Задание №1555

С высоты 40 м тело брошено горизонтально со скоростью 5 м/с. Определите дальность полёта и скорость тела в момент удара о землю.

Решение

Дано:
h = 40 м;
$v_{0} = 5$ м/с;
g ≈ 10 $м/с^{2}$.
Найти:
l − ?
v − ?
Решение:
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = 0$; $g_{y} = g$; y = h; $y_{0} = 0$, то
$h =\frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
$t = \sqrt{\frac{2 * 40}{10}} = 2,8$ с;
$v_{y} = gt$;
$v_{y} = 10 * 2,8= 28$ м/с;
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}$; x = l, то:
$l = v_{0}t$;
l = 5 * 2,8 = 14 м;
Найдем скорость тела в момент удара о землю по теореме Пифагора:
$V^{2} = V_{y}^{2} + V_{0}^{2}$;
$V = \sqrt{V_{y}^{2} + V_{0}^{2}}$;
$V = \sqrt{28^{2} + 5^{2}} = 28,4$ м/с.
Ответ: 14 м; 28,4 м/с.

Задание №1556

Ракета на высоте Н = 50 км после прекращения работы двигателей приобрела горизонтальную скорость v = 1 км/с. Определите дальность полёта ракеты АС, если АВ = З0 км (рис. 249). Принять g = 10 $м/с^{2}$. Кривизну земной поверхности не учитывать.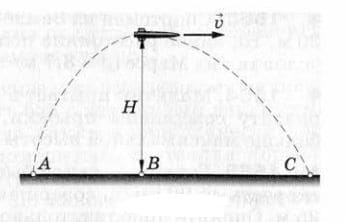
рис. 249

Решение

Дано:
H = 50 км;
v = 1 км/с;
AB = 30 км;
g ≈ 10 $м/с^{2}$.
Найти:
AC − ?
СИ:
H = 50 000 м;
v = 1 000 м/с.
Решение:
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = 0$; $g_{y} = g$; y = h; $y_{0} = 0$, то
$h =\frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
$t = \sqrt{\frac{2 * 50 000}{10}} = 100$ с;
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}$; x = BC, то:
$BC= v_{0}t$;
BC = 1 000 * 100 = 100 000 м = 100 км.
AC = AB + BC;
AC = 30 + 100 = 130 км.
Ответ: 130 км.

Задание №1557

Вертолёт летит на высоте 80 м над поверхностью земли. С какой горизонтальной скоростью должен лететь вертолёт, чтобы, сбросив груз, попасть точно в цель, если он летит на расстоянии 400 м от цели?

Решение

Дано:
h = 80 м;
l = 400 м;
g ≈ 10 $м/с^{2}$.
Найти:
$v_{0}$ − ?
Решение: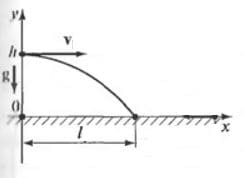
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = 0$; $g_{y} = g$; y = h; $y_{0} = 0$, то
$h =\frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}$; x = l, то:
$l = v_{0}t$;
$v_{0} = \frac{l}{t} = \frac{l}{\sqrt{\frac{2h}{g}}} = {l}{\sqrt{\frac{g}{2h}}}$;
$v_{0} = 400 * {\sqrt{\frac{10}{2 * 80}}} = 100$ м/с;
Ответ: 100 м/с.

Задание №1558

Дальность полёта тела, брошенного в горизонтальном направлении со скоростью 5 м/с, равна высоте бросания. С какой высоты брошено тело?

Решение

Дано:
h = l;
$v_{0}$ = 5 м/с;
g ≈ 10 $м/с^{2}$.
Найти:
h − ?
Решение: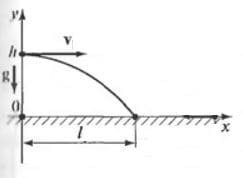
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}$; x = l, то:
$l = v_{0}t$;
$t = \frac{l}{v_{0}} = \frac{h}{v_{0}} $;
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$y = y_{0} + v_{0y}t + \frac {g_{y}t^{2}}{2}$;
Т.к. $v_{0y} = 0$; $g_{y} = g$; y = h; $y_{0} = 0$, то
$h =\frac {gt^{2}}{2}$;
$2h = gt^{2}$;
$t^{2} = \frac{2h}{g}$;
$t = \sqrt{\frac{2h}{g}}$;
$\frac{h}{v_{0}} = \sqrt{\frac{2h}{g}}$;
$\frac{h^{2}}{v_{0}^{2}} = \frac{2h}{g}$;
$\frac{h^{2}}{2h} = \frac{v_{0}^{2}}{g}$;
$h = \frac{2v_{0}^{2}}{g}$;
$h = \frac{2 * 5^{2}}{10} = 5$ м.
Ответ: 5 м.

Задание №1559

С воздушного шара, поднимающегося со скоростью 10 м/с, сбрасывают груз, который достигает поверхности земли через 8 с. На какой высоте находился шар в момент сбрасывания груза?

Решение

Дано:
t = 8 c;
$v_{0} = - 10$ м/с;
g ≈ 10 $м/с^{2}$.
Найти:
h − ?
Решение:
Уравнение движения:
$h = v_{0}t + \frac {gt^{2}}{2}$;
$h = -10 * 8 + \frac {10 * 8^{2}}{2} = 240$ м.
Ответ: 240 м.

Задание №1560

Определите высоту Останкинской телевизионной башни, если шарик, падая с башни без начальной скорости, последние 185 м пути пролетел за 2 с.

Решение

Дано:
t = 2 c;
h = 185 м;
g ≈ 10 $м/с^{2}$.
Найти:
H − ?
Решение:
Уравнение движения:
$h = v_{0}t + \frac {gt^{2}}{2}$;
Найдем скорость шарика на высоте h = 185 м:
$v_{0}t = h - \frac {gt^{2}}{2}$;
$v_{0} = \frac{h - {\frac {gt^{2}}{2}}}{{t}} = \frac{2h - gt^{2}}{2t}$;
$v_{0} = \frac{2 * 185 - 10 * 2^{2}}{2 * 2} = 82,5$ м/с;
Найдем конечную скорость шарика:
$h = \frac{v^{2} - v_{0}^{2}}{2g}$;
$2hg = v^{2} - v_{0}^{2}$;
$v^{2} = 2hg + v_{0}^{2}$;
$v = \sqrt {2hg + v_{0}^{2}}$;
$v = \sqrt {2 * 185 * 10 + 82,5^{2}} = 102,5$;
Найдем высоту, с которой упал шарик без начальной скорости:
$h = \frac{102,5^{2} - 0^{2}}{2 * 10} = 525$ м.
Ответ: 525 м.

Задание №1561

Два тела начали свободно падать с одной и той же высоты одно вслед за другим через 5 с. Через какое время, считая от начала движения первого тела, расстояние между телами будет равно 200 м?

Решение

Дано:
$Т = t - 5$;
h = 200 м;
g ≈ 10 $м/с^{2}$.
Найти:
t − ?
Решение:
$h = v_{0}t + \frac {gt^{2}}{2}$;
Так как тело падает без начальной скорости, то $v_{0} = 0$;
Расстояние, которое пройдет первое тело за время t, равно:
$h_{1} = \frac {gt^{2}}{2}$;
Расстояние, которое пройдет второе тело за время t, равно:
$h_{2} = \frac {gТ^{2}}{2} = \frac {g * (t-5)^{2}}{2} $;
Расстояние между телами за время t будет равно:
$h = h_{1} - h_{2}$;
$h = \frac {gt^{2}}{2} - \frac {g(t-5)^{2}}{2} = \frac {gt^{2} - g(t-5)^{2}}{2} = \frac {gt^{2} - g(t^{2} - 10t + 25)}{2} = \frac {gt^{2} - gt^{2} + 10gt - 25g}{2} = \frac {g * (10t - 25)}{2}$;
2h = g * (10t − 25);
$10t-25 = \frac{2h}{g}$;
$10t = \frac{2h}{g} + 25$;
$t =\frac{ \frac{2h}{g} + 25}{10} = \frac{ 2h + 25g}{10g}$;
$t = \frac{2 * 200 + 25 * 10}{10 * 10} = 6,5$ с.
Ответ: 6,5 с.

Задание №1562

С какой скоростью надо бросать копьё под углом 30° к горизонту, чтобы дальность полёта была равной 68 м?

Решение

Дано:
α = 30°;
l = 68 м;
g ≈ 10 $м/с^{2}$.
Найти:
$v_{0}$− ?
Решение: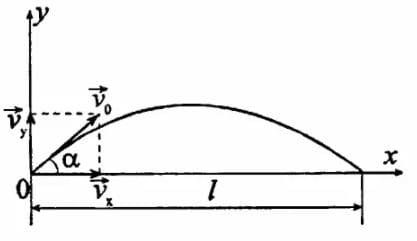
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{0y} + g_{y}t$;
Т.к. $v_{0y} = v_{0}sinα$; $g_{y} = -g$; $v_{y} = 0$, то
$0 = v_{0}sinα - gt$;
$v_{0}sinα = gt$;
$t = \frac{v_{0}sinα}{g}$
В данной системе отсчета движение вдоль горизонтальной оси Оx равномерное.
$v_{x} = v_{0x}$;
$x = x_{0} + v_{0x}t$;
Т.к. $x_{0} = 0$; $v_{0x} = v_{0}sosα$; x = l, то:
$l = v_{0}sosα * 2t = v_{0}sosα * 2 * \frac{v_{0}sinα}{g} = \frac{2v_{0}^{2}sinsαcosα}{g}$;
$lg = 2v_{0}^{2}sinsαcosα$;
$v_{0}^{2} = \frac{lg}{2sinsαcosα}$;
$v_{0} = \sqrt{\frac{lg}{2sinsαcosα}} = \sqrt{\frac{68 * 10}{2sins30°cos30°}} = \sqrt{\frac{68 * 10}{2 * 0,5 * 0,87}} = 27,9$ м/с.
Ответ: 27,9 м/с.