Задание №1600

Почему жидкость легче переливать из сосуда в сосуд на Земле, чем на Луне? Действует ли сила тяготения между космонавтом и Землей, когда космонавт находится в состоянии невесомости в космическом корабле?

Решение

Жидкость обладает текучестью, между жидкостью и Землей существует сила тяготения, поэтому жидкость стремится к центру масс Земли. Сила тяжести на Земле больше, поэтому жидкость легче переливать из сосуда в сосуд на Земле, чем на Луне.
Сила тяготения между телами существует всегда, значит она действует и между космонавтом и Землей. В данном случае состояние невесомости космонавта обуславливается тем, что сила тяготения уравновешивается центробежной силой.

Задание №1601

Изменится ли сила тяжести, действующая на медный шар, если его опустить в воду; в керосин?

Решение

Не изменится, так как сила тяжести зависит от массы и ускорения свободного падения.

Задание №1602

Два тела равной массы находятся на расстоянии 100 м. Какой должна быть масса этих тел, чтобы они притягивались силой $6,67 * 10^{-9}$ Н?

Решение

Дано:
$m_{1} = m_{2}$;
r = 100 м;
F = $6,67 * 10^{-9}$ Н;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
$m_{1}$ − ?
$m_{2}$ − ?
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
$F * r^{2}= G * m_{1}m_{2}$;
$m_{1}m_{2} = \frac{F * r^{2}}{G}$;
Т.к. $m_{1} = m_{2}$, то
$m_{1}^{2} = \frac{F * r^{2}}{G}$;
$m_{1} = \sqrt{\frac{F * r^{2}}{G}}$;
$m_{1} = \sqrt{\frac{6,67 * 10^{-9} * 100^{2}}{6,67 * 10^{-11}}} = 1000 кг$.
$m_{1} = m_{2} = 1000 кг$.
Ответ: 1000 кг.

Задание №1603

Рассчитайте силу притяжения между двумя телами массами 60 и 50 кг, учитывая, что они имеют сферическую форму и расстояние между их центрами масс равно 1 м.

Решение

Дано:
$m_{1} = 60$ кг;
$m_{2} = 50$ кг;
r = 1 м;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
F − ?
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
$F = 6,67 * 10^{-11} * \frac{60 * 50}{1^{2}} = 2 * 10^{-7}$ Н.
Ответ: $2 * 10^{-7}$ Н.

Задание №1604

В одном из опытов Г. Кавендиша, упрощённая схема установки которого изображена на рисунке 250, сила притяжения между свинцовым шаром массой 155 кг и шариком массой 730 г на расстоянии 18,4 см была равна $2,2 * 10^{-7}$ Н. Какое значение гравитационной постоянной получил учёный в этом опыте?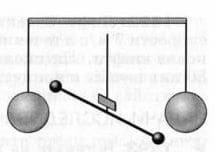
рис. 250

Решение

Дано:
$m_{1} = 155$ кг;
$m_{2} = 730$ г;
r = 18,4 см;
F = $2,2 * 10^{-7}$ Н.
Найти:
G − ?
СИ:
$m_{2} = 0,73$ кг;
r = 0,184 м;
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
$Fr^{2} = G * m_{1}m_{2}$;
$G = \frac{Fr^{2}}{m_{1}m_{2}}$;
$G = \frac{2,2 * 10^{-7} * 0,184^{2}}{155 * 0,73} = 6,58 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Ответ: $6,58 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.

Задание №1605

С какой силой притягиваются два железнодорожных вагона массой 70 т каждый, если расстояние между ними 200 м?

Решение

Дано:
$m_{1} = m_{2} = 70$ т;
r = 200 м;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
F − ?
СИ:
$m_{1} = m_{2} = 7 * 10^{4}$ кг.
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
$F = 6,67 * 10^{-11} * \frac{7 * 10^{4} * 7 * 10^{4}}{200^{2}} = 6,67 * 10^{-11} * \frac{4,9 * 10^{9}}{4 * 10^{4}} = 6,67 * 10^{-11} * 1,225 * 10^{5} = 8,2 * 10^{-6}$ Н.
Ответ: $8,2 * 10^{-6}$ Н.

Задание №1606

Найдите силу гравитационного притяжения, действующую между Землёй и Луной, если масса Земли равна $6 * 10^{24}$ кг, а масса Луны − $7,2 * 10^{22}$ кг. Расстояние от Земли до Луны $3,8*10^{8}$ м.

Решение

Дано:
$m_{1} = 6 * 10^{24}$ кг;
$m_{2} = 7,2 * 10^{22}$ кг;
$r = 3,8*10^{8}$ м;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
F − ?
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
$F = 6,67 * 10^{-11} * \frac{6 * 10^{24} * 7,2 * 10^{22}}{(3,8*10^{8})^{2}} = 6,67 * 10^{-11} * \frac{4,32 * 10^{47}}{1,444*10^{17}} = 6,67 * 10^{-11} * 2,99 *10^{30} = 2 * 10^{20}$ Н.
Ответ: $2 * 10^{20}$ Н.

Задание №1607

Во сколько раз малая планета Плутон притягивается к Солнцу слабее Земли, если Плутон удалён от Солнца на расстояние в 40 раз большее, чем Земля? Массы Земли и Плутона приблизительно одинаковы.

Решение

Дано:
$m_{1} ≈ m_{2}$;
$\frac{r_{1}}{r_{2}} = 40$.
Найти:
$\frac{F_{2}}{F_{1}}$ − ?
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
$\frac{F_{2}}{F_{1}} = \frac{\frac{G * m_{2}m_{c}}{r_{2}^{2}}}{ \frac{G * m_{1}m_{c}}{r_{1}^{2}}}= \frac{m_{2}r_{1}^{2}}{m_{1}r_{2}^{2}} = \frac{m_{2}}{m_{1}} * (\frac{r_{1}}{r_{2}})^{2}$;
Т.к. $m_{1} ≈ m_{2}$, то
$\frac{F_{2}}{F_{1}} = (\frac{r_{1}}{r_{2}})^{2} = 40^{2} = 1600$.
Ответ: В 1600 раз Плутон притягивается к Солнцу слабее Земли.

Задание №1608

На каком расстоянии от поверхности Земли сила притяжения космического корабля к ней станет в 25 раз меньше, чем на поверхности Земли?

Решение

Дано:
$\frac{F_{1}}{F_{2}} = 25$.
Найти:
h − ?
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
При удалении корабля на расстояние h, расстояние до центра масс Земли станет равным:
$r_{2} = r + h$;
Найдем расстояние от поверхности Земли до космического корабля:
$\frac{F_{1}}{F_{2}} = \frac{ \frac{G * m_{1}m_{2}}{r^{2}}}{\frac{G * m_{1}m_{2}}{r_{2}^{2}}} = \frac{r_{2}^{2}}{r^{2}} = \frac{(r + h)^{2}}{r^{2}} = 25$;
$(r + h)^{2} = 25 * r^{2}$;
$r + h= \sqrt{25 * r^{2}} = 5r$;
h = 5r − r = 4 r.
Ответ: На расстоянии 4 земных радиусов.

Задание №1609

Во сколько раз уменьшится сила притяжения к Земле космического корабля при его удалении от поверхности Земли на расстояние, равное 5 радиусам Земли?

Решение

Дано:
h = 5r;
Найти:
$\frac{F_{1}}{F_{2}}$ − ?
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
При удалении корабля на расстояние h, расстояние до центра масс Земли станет равным:
$r_{2} = r + h = r + 5r = 6r$;
Найдем расстояние от поверхности Земли до космического корабля:
$\frac{F_{1}}{F_{2}} = \frac{ \frac{G * m_{1}m_{2}}{r^{2}}}{\frac{G * m_{1}m_{2}}{r_{2}^{2}}} = \frac{r_{2}^{2}}{r^{2}} = \frac{(6r)^{2}}{r^{2}} = \frac{36r^{2}}{r^{2}} = 36$.
Ответ: В 36 раз.

Задание №1610

Определите точку на прямой, соединяющей Землю и Луну, в которой равнодействующая сил притяжения Земли и Луны равна нулю. Расстояние между центрами Земли и Луны равно 60 земным радиусам, а масса Луны в 81 раз меньше массы Земли.

Решение

Дано:
$F_{1} = F_{2}$;
$r = 60R$;
$M_{з} = 81M_{л}$.
Найти:
n − ?
Решение:
По закону всемирного тяготения:
$F = G * \frac{m_{1}m_{2}}{r^{2}}$;
Пусть тело находится от Земли на расстоянии n радиусов, тогда расстояние до Луны равно $(60 - n)R$.
Найдем точку равновесия:
$G * \frac{mM_{з}}{(nR)^{2}} = G * \frac{mM_{л}}{((60 - n)R)^{2}}$;
$\frac{M_{з}}{n^{2}} = \frac{M_{л}}{(60 - n)^{2}}$;
$(60 - n)^{2} * M_{з} = n^{2}M_{л}$;
$(60 - n)^{2} * 81M_{л} = n^{2}M_{л}$;
$(9 * (60 - n))^{2} * M_{л} = n^{2}M_{л}$;
9 * (60 − n) = n;
540 − 9n = n;
10n = 540;
$n = \frac{540}{10} = 54$ радиусов до Земли или
(60 − 54)R = 6 радиусов до Луны.
Ответ: Тело будет притягиваться с одинаковой силой в точке, находящейся на расстоянии 6 земных радиусов от центра Луны или 54 земных радиусов от центра Земли.