Задание №1777

Груз, колеблющийся на пружине, за 8 с совершил 32 колебания. Найдите период и частоту колебаний.

Решение

Дано:
t = 8 c;
N = 32 колебания.
Найти:
T − ?
ν − ?
Решение:
$T = \frac{t}{N}$;
$T = \frac{8}{32} = 0,25$ с;
$ν = \frac{N}{t}$;
$ν = \frac{32}{8} = 4$ Гц.
Ответ: 0,25 с; 4 Гц.

Задание №1778

Маятник совершает 9 колебаний за 18 с. Определите период и частоту колебаний. Постройте график колебаний, если амплитуда равна 10 см.

Решение

Дано:
t = 18 c;
N = 9 колебаний;
A = 10 см.
Найти:
T − ?
ν − ?
Решение:
$T = \frac{t}{N}$;
$T = \frac{18}{9} = 2$ с;
$ν = \frac{N}{t}$;
$ν = \frac{9}{18} = 0,5$ Гц.
Ответ: 2 с; 0,5 Гц.

Амплитуда колебаний в СИ измеряется в метрах.
СИ: A = 0,1 м
График колебаний маятника.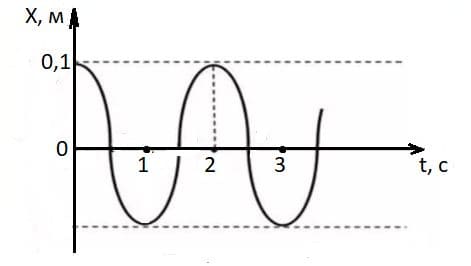

Задание №1779

Период колебания крыльев шмеля 5 мс, а частота колебаний крыльев комара 600 Гц. Определите, какое насекомое и на сколько больше сделает взмахов крыльями при полёте за 1 мин.

Решение

Дано:
$T_{ш} = 5$ мс;
$ν_{к} = 600$ Гц;
t = 1 мин.
Найти:
|$N_{к} - N_{ш}$|− ?
СИ:
$T_{ш} = 0,005$ с;
t = 60 с.
Решение:
$T = \frac{t}{N}$;
$N = \frac{t}{T}$;
$N_{ш} = \frac{60}{0,005} = 12 000$ взмахов;
$ν = \frac{N}{t}$;
N = tν;
$N_{к} = 60 * 600 = 36 000$ взмахов.
$N_{к}>N_{ш}$;
|$N_{к} - N_{ш}$| = 36 000 − 12 000 = 24 000 взмахов.
Ответ: Комар сделает на 24 000 взмахов больше, чем шмель.

Задание №1780

По графику зависимости смещения колеблющейся точки от времени, изображённому на рисунке 279, определите амплитуду, период и частоту колебаний.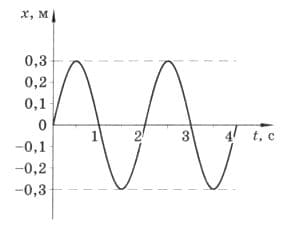
рис. 279

Решение

Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний.
A = 0,3 м.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
T = 2 c.
Число колебаний в единицу времени называется частотой колебаний.
$ν = \frac{1}{T}$;
$ν = \frac{1}{2} = 0,5$ Гц.
Ответ: 0,3 м; 2 с; 0,5 Гц.

Задание №1781

Определите амплитуду, период и частоту колебали по графику зависимости смещения колеблющейся точки от времени, изображённому на рисунке 280.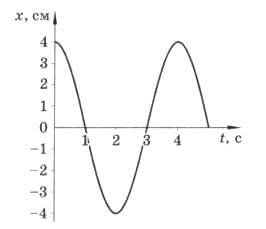
рис. 280

Решение

Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний.
A = 4 см.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
T = 4 c.
Число колебаний в единицу времени называется частотой колебаний.
$ν = \frac{1}{T}$;
$ν = \frac{1}{4} = 0,25$ Гц.
Ответ: 4 см; 4 с; 0,25 Гц.

Задание №1782

По графику колебаний (рис. 281) определите начальное смещение тела, амплитуду и период колебания. Напишите уравнение колебаний.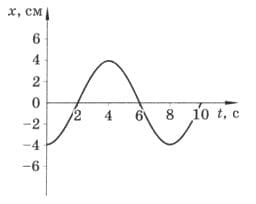
рис. 281

Решение

$x_{0} = -4$ см.
Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний.
A = 4 см.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
T = 8 c.
Уравнение гармонических колебаний:
$x = x_{0}cos ( \frac{2π}{T}t)$;
$x = -4cos ( \frac{2π}{8}t)$;
$x = -4cos\frac{πt}{4}$ (cм).
Ответ: − 4 см; 4 см; 8 с; $x = -4cos\frac{πt}{4}$ (cм).

Задание №1783

Рассчитайте период колебания математического маятника, длина нити которого равна 2,5 м.

Решение

Дано:
l = 2,5 м;
g ≈ 10 $м/с^{2}$.
Найти:
T − ?
Решение:
$T = 2π\sqrt{\frac{l}{g}}$;
$T = 2 * 3,14\sqrt{\frac{2,5}{10}} = 3,14$ с.
Ответ: 3,14 с.

Задание №1784

Металлический брусок массой 125 г совершает колебания на пружине жёсткостью 50 Н/м. Чему равен период колебания бруска?

Решение

Дано:
m = 125 г;
k = 50 Н/м.
Найти:
T − ?
СИ:
m = 0,125 кг.
Решение:
$T = 2π\sqrt{\frac{m}{k}}$;
$T = 2 * 3,14\sqrt{\frac{0,125}{50}} = 0,314$ с.
Ответ: 0,314 с.

Задание №1785

Как изменится частота колебаний математического маятника, если длину его нити увеличить в 9 раз; уменьшить в 25 раз?

Решение

1. Дано:
$l_{2} = 9l_{1}$.
Найти:
$\frac{ν_{1}}{ν_{2}}$ − ?
Решение:
$T = 2π\sqrt{\frac{l}{g}}$;
$ν = \frac{1}{T} = \frac{1}{2π}\sqrt{\frac{g}{l}}$;
$\frac{ν_{1}}{ν_{2}} = \frac{\frac{1}{2π}\sqrt{\frac{g}{l_{1}}}}{\frac{1}{2π}\sqrt{\frac{g}{l_{2}}}} = \sqrt{\frac{l_{2}}{l_{1}}}$;
$\frac{ν_{1}}{ν_{2}} = \sqrt{\frac{9l_{1}}{l_{1}}} = \sqrt{9} = 3$.
Ответ: Частота уменьшится в 3 раза.

2. Дано:
$l_{1} = 25l_{2}$.
Найти:
$\frac{ν_{2}}{ν_{1}}$ − ?
Решение:
$T = 2π\sqrt{\frac{l}{g}}$;
$ν = \frac{1}{T} = \frac{1}{2π}\sqrt{\frac{g}{l}}$;
$\frac{ν_{2}}{ν_{1}} = \frac{\frac{1}{2π}\sqrt{\frac{g}{l_{2}}}}{\frac{1}{2π}\sqrt{\frac{g}{l_{1}}}} = \sqrt{\frac{l_{1}}{l_{2}}}$;
$\frac{ν_{2}}{ν_{1}} = \sqrt{\frac{25l_{2}}{l_{2}}} = \sqrt{25} = 5$.
Ответ: Частота увеличится в 5 раз.