Задание №1690

Докажите, что легче − удерживать тело на наклонной плоскости или двигать его по ней равномерно вверх.

Решение

Тело легче удерживать на наклонной плоскости. В этом случае сила трения направлена вверх и совпадает с приложенной силой. Следовательно, приложенная сила может быть незначительной. Если тело двигать вверх по наклонной плоскости, то сила трения будет направлена противоположно движению, а поэтому будет препятствовать ему. Следовательно, приложенная сила должна быть больше, чем в первом случае.

Задание №1691

Два тела висят на нитях разной длины и описывают горизонтальные окружности. Противоположные концы нитей неподвижны. Докажите, что время обращения обоих тел всегда одинаковое, если конусы, описываемые нитями, имеют одинаковую высоту (задача Гюйгенса).

Решение

Дано:
$l_{1}$;
$l_{2}$;
$h_{1} = h_{2}$.
Доказать:
$T_{1} = T_{2}$.
Решение: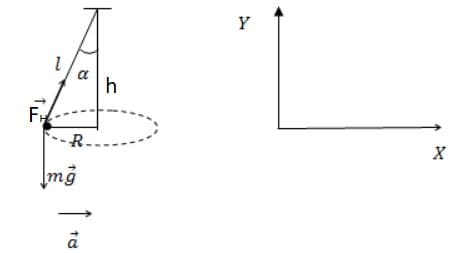
Пусть l − длина нити, α — угол нити с вертикалью, R — расстояние от тела до оси, h − высота конуса.
Изобразим все силы, действующие на тело: сила тяжести $\overset{→}{mg}$, сила натяжения нити $\overset{→}{F_{н}}$.
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{F_{н}}$;
Спроецируем уравнение на координатные оси:
ось X: $ma = Tsinα = \frac{mv^{2}}{R}$;
ось Y: mg = Tcosα;
$tgα = \frac{\frac{mv^{2}}{R}}{mg} = \frac{v^{2}}{Rg}$
$v^{2} = gRtgα$;
$v = \sqrt{gRtgα}$;
Радиус окружности, описываемой телом, равен:
R = lsinα;
Найдем период обращения:
$T = \frac{2πR}{v} = \frac{2πR}{\sqrt{gRtgα}} = 2π\sqrt{\frac{R}{g}ctgα} = 2π\sqrt{\frac{lsinα}{g}ctgα} = 2π\sqrt{\frac{lcosα}{g}} = 2π\sqrt{\frac{h}{g}}$.
$T_{1} = 2π\sqrt{\frac{h_{1}}{g}}$;
$T_{2} = 2π\sqrt{\frac{h_{2}}{g}}$;
Если $h_{1} = h_{2}$, то $T_{1} = T_{2} = 2π\sqrt{\frac{h}{g}}$.
Таким образом, время обращения обоих тел всегда одинаковое, если конусы, описываемые нитями, имеют одинаковую высоту

Задание №1692

Верёвка пренебрежимо малой массы перекинута через блок, вращающийся без трения. За один конец верёвки держится обезьяна, к другому концу прикреплено зеркало того же веса, что и обезьяна. Может ли обезьяна сместиться относительно своего изображения в зеркале, если она:
а) будет взбираться по верёвке вверх;
б) будет опускаться по верёвке вниз;
в) отпустит верёвку?

Решение

а) Если обезьяна будет взбираться по верёвке вверх, зеркало будет подниматься вверх с тем же ускорением, что и обезьяна, так как на обезьяну и зеркало действует одинаковая сила тяжести, а это означает что эти силы взаимоуничтожаются, и в итоге обезьянка просто тянет зеркало к себе, что в условиях пренебрежения весом веревки и силой тяжести приведёт к равномерному движению вверх двух данных тел. Таким образом, обезьяна не может сместиться относительно своего изображения в зеркале.

б) Аналогично пункту а). Если обезьяна будет опускаться по верёвке вниз, зеркало будет опускаться вниз с тем же ускорением, что и обезьяна, так как на обезьяну и зеркало действует одинаковая сила тяжести, а это означает что эти силы взаимоуничтожаются, и в итоге обезьянка просто оттягивает зеркало от себя, что в условиях пренебрежения весом веревки и силой тяжести приведёт к равноемрному движению вниз двух данных тел. Таким образом, обезьяна не может сместиться относительно своего изображения в зеркале.

в) Если обезьяна отпустит верёвку, то обезьяна и зеркало будут падать с одним и тем же ускорением свободного падения. Таким образом, обезьяна не будет смещаться относительно своего изображения в зеркале.

Задание №1693

Известно, что велосипедист на повороте наклоняется. Угол наклона зависит от скорости движения (возрастает с её увеличением) и от радиуса окружности (возрастает с его уменьшением при одной и той же скорости движения). Зависит ли угол наклона от массы велосипедиста, т.е. должен ли угол наклона быть одинаковым при одной и той же скорости для отца и его десятилетнего сына? Ответ обоснуйте.

Решение

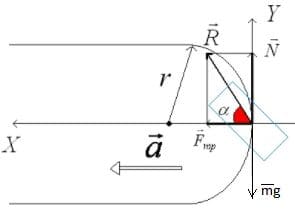Изобразим все силы, действующие на велосипедиста: сила тяжести $\overset{→}{mg}$, сила реакции опоры $\overset{→}{N}$, сила, которая может обеспечить движение велосипедиста по окружности − сила трения $\overset{→}{F_{тр}}$.
Согласно законам статики, для того, чтобы велосипедист не потерял равновесие, необходимо, чтобы равнодействующая сил $\overset{→}{N}$ и $\overset{→}{F_{тр}}$ была направлена по прямой, проходящей через центр тяжести велосипедиста, эти силы направлены под углом 90° друг к другу.
$tgα = \frac{F_{тр}}{N} =\frac{μN}{N} = μ$;
Запишем второй закон Ньютона в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{F_{тр}} + \overset{→}{N}$;
Спроецируем уравнение на координатные оси:
ось X: $ma = F_{тр} = μN$;
ось Y: 0 = N − mg;
N = mg;
ma = μmg;
$a = μg = \frac{v^{2}}{R}$;
$ μ = \frac{v^{2}}{gR}$;
$tgα = \frac{v^{2}}{gR}$;
$ α= arctg (\frac{v^{2}}{gR})$.
Таким образом, угол наклона зависит от скорости движения, радиуса окружности и не зависит от массы велосипедиста.

Задание №1694

В рассказе Марка Твена «Укрощение велосипеда» написано: «Если мне случалось падать направо, я, следуя вполне естественному убеждению, круто заворачивал руль налево, нарушая, таким образом, закон природы. Закон требовал обратного: переднее колесо нужно поворачивать в ту сторону, куда падаешь». Почему велосипед надо наклонять в сторону поворота?

Решение

Если велосипед наклонять направо, то произойдёт поворот, а не падение, так как возникнет сила, создающая центростремительное ускорение.