Задание №1404

Инспектор ГИБДД на мотоцикле, двигаясь со скоростью 126 км/ч, догоняет
грузовой автомобиль, движущийся со скоростью 54 км/ч. Укажите начальные координаты мотоцикла и автомобиля, приняв за начало координат пост ГИБДД (рис. 219). Напишите уравнения движения мотоцикла и автомобиля. Определите, за какое время мотоцикл догонит автомобиль. Постройте графики изменения координат мотоцикла и автомобиля.
рис. 219

Решение

Дано:
$v_{м} = 126$ км/ч;
$v_{гр} = 54$ км/ч.
Найти:
$x_{0м}$ − ?
$x_{0гр}$ − ?
$x(t)_{м}$ − ?
$x(t)_{гр}$ − ?
t − ?
СИ:
$v_{м} = 35$ м/с;
$v_{гр} = 15$ м/с.
Решение:
Начальные координаты тел:
$x_{0м} = 300$ м;
$x_{0гр} = x_{0м} + 1200 = 300 +1200 = 1500$ м;
Составим уравнения движения:
$x(t) = x_{o} + v_{x}t$;
$x(t)_{м} = 300 + 35t$ м;
$x(t)_{гр} = 1500 + 15t$ м;
Найдем время до встречи мотоцикла с автомобилем:
$x_{м} = x_{гр}$;
$300 + 35t = 1500 + 15t$;
20t = 1200;
$t = \frac{1200}{20} = 60$ c.
Ответ: 300 м; 1500 м; $x_{м} = 300 + 35t$ м; $x_{гр} = 1500 + 15t$ м; 60 с.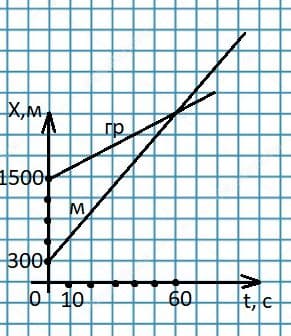

Задание №1405

Движение двух самолётов, летящих параллельными курсами, задано уравнениями $х_{1} = 150t$ (м), $х_{2} = 8400 - 250t$ (м). Как движутся самолёты − равномерно или неравномерно? Чему равны модули скоростей движения самолётов? Каково направление их скоростей? На каком расстоянии друг от друга в начальный момент времени находятся самолёты? Через какое время они встретятся?

Решение

Дано:
$х_{1} = 150t$ (м);
$х_{2} = 8400 - 250t$ (м).
Найти:
$v_{1}$ − ?
$v_{2}$ − ?
$Δx_{0}$ − ?
t − ?
Решение:
При прямолинейном равномерном движении координата тела х(t) зависит от времени формулой: $x(t) = x_{o} + v_{x}t$, где $x_{0}$ − начальная координата тела, $v_{x}$ − скорость движения.
Самолеты движутся равномерно прямолинейно.
$v_{1} = 150$ м/с;
$v_{2} = 250$ м/с.
Скорости движения самолетов направлены противоположно друг другу.
Расстояние между самолетами в начальный момент времени
$Δx_{0} = x_{0} (2) - x_{0} (1) = 8400 - 0 = 8400$ м;
Найдем время встречи двух самолетов:
$х_{1} = х_{2}$;
$150t = 8400 - 250t$;
$400t = 8400$;
$t = \frac{8400}{400} = 21$ с.
Ответ: 150 м/с; 250 м/с; скорости движения самолетов направлены противоположно друг другу; 8400 м; 21 с.

Задание №1406

Движение двух тел задано уравнениями $х_{1} = 20t$ (м), $х_{2} = 250 - 5t$ (м). Найдите:
а) место и время встречи этих тел;
б) координату второго тела в момент времени, когда координата первого тела была равна 100 м;
в) в какой момент времени расстояние между телами составляло 125 м.
Учесть, что тела начали двигаться одновременно.

Решение

Дано:
$х_{1} = 20t$ (м);
$х_{2} = 250 - 5t$ (м).
Найти:
x и t встречи − ?
$x_{2(x_{1} = 100)}$ − ?
$t_{Δx=125}$ − ?
Решение:
а) В момент встречи тела имеют равную координату. Значит правые части уравнений можно приравнять. Найдем время встречи двух тел:
$х_{1} = х_{2}$;
20t = 250 − 5t;
25t = 250;
$t = \frac{250}{25} = 10$ с.
Подставим время в уравнение движения первого тела:
$x_{1} = 20 * 10 = 200$ м.
б) Найдем координату второго тела в момент времени, когда координата первого тела была равна 100 м;
$х_{1} = 20t$;
100 = 20t;
$t = \frac{100}{20} = 5$ с;
$х_{2(t=5)} = 250 - 5 * 5 = 225$ (м).
в) Найдем в какой момент времени расстояние между телами составляло 125 м.
$Δx = х_{2} - х_{1}$;
125 = 250 − 5t − 20t;
25t = 125;
$t = \frac{125}{25}$;
t = 5 с.
Ответ: 10 с; в 200 м от начального положения первого тела; 225 м; 5 с.

Задание №1407

Расстояние между двумя городами равно 280 км. Из этих городов начали одновременно двигаться навстречу друг другу два автомобиля: один − со скоростью 90 км/ч, другой − со скоростью 72 км/ч. Постройте графики движения автомобилей и по графикам определите время их встречи и расстояние от места встречи до каждого из городов.

Решение

Дано:
s = 280 км;
$v_{1} = 90$ км/ч;
$v_{2} = 72$ км/ч;
Найти:
x и t встречи − ?
Решение:
При прямолинейном равномерном движении координата тела х(t) зависит от времени формулой: $x(t) = x_{o} + v_{x}t$, где $x_{0}$ − начальная координата тела, $v_{x}$ − скорость движения.
Составим уравнения движения:
$x_{1} = 90t$;
$x_{2} = 280 - 72t$.
Построим графики движения автомобилей:
Согласно графику время встречи ≈ 1,75 ч; место встречи − ≈ 156 км от города выезда 1−го автомобиля, ≈ 124 км от города выезда 2−го автомобиля.
Проверим полученные координатным методом.
В момент встречи тела имеют равную координату. Значит правые части уравнений можно приравнять. Найдем время встречи двух тел:
$х_{1} = х_{2}$;
90t = 280 − 72t;
162t = 280;
$t = \frac{280}{162} = 1,73$ ч.
Подставим время в уравнение движения:
$x_{1} = 90 * 1,73 = 156$ км.
Ответ: 1,73 ч; ≈ 156 км от города выезда 1−го автомобиля, ≈ 124 км от города выезда 2−го автомобиля.