Задание №1731
С воздушного шара, неподвижно висящего в воздухе, свободно свешивается лестница (рис. 269). По ней начинает взбираться человек. При этом шар будет подниматься или опускаться?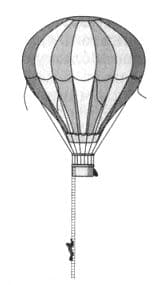 рис. 269
рис. 269
Решение
Шар будет опускаться. Под действием череды импульсов (рывков) при подъёме человека шар опустится, а затем вернётся на исходную высоту.
Задание №1732
Две одинаковые тележки, на которых стоят два дворника с равными массами, движутся по инерции с одинаковыми скоростями параллельно друг другу. В некоторый момент времени на тележки начинает равномерно падать снег. Дворник, стоящий на одной тележке, всё время сбрасывает снег вбок, а дворник, стоящий на другой тележке, нет. Какая из тележек быстрее пройдет одно и то же расстояние?
Решение
Дано:
$v_{1} = v_{2} = v$;
$S_{1} = S_{2} = S$;
$M_{1} = M_{2} = M$.
Найти:
$t_{1} > t_{2}$ − ?
Решение:
1. Рассмотрим тележку, с которой дворник сбрасывает снег. Так как вдоль горизонтальной оси на систему «тележка−дворник» никакие внешние силы не действуют, то можно записать закон сохранения импульса системы «тележка−дворник» в проекциях на направление движения тележки. Пусть за определённый промежуток времени на тележку массой M выпала первая порция снега массой m:
$Mv_{0} = (M + m) v_{1}'$.
Скорость тележки стала:
$ v_{1}' = \frac{Mv_{0}}{M + m}$;
Затем дворник сбросил этот снег перпендикулярно направлению движения, импульс тележки стал $Mv_{1}'$ (сбрасывание снега в стороны не меняет скорости тележки). Следом упала вторая порция снега:
$Mv_{1}' = (M + m) * v_{2}'$.
Скорость тележки стала:
$ v_{2}' = \frac{Mv_{1}'}{M + m} = \frac{M * \frac{Mv_{0}}{M + m}}{M + m} = \frac{M^{2}v_{0}}{(M + m)^{2}} = (\frac{M}{(M + m)})^{2} * v_{0}$;
Дворник вновь сбросил эту порцию снега. Затем упала третья порция и т. д. Скорость тележки после n−ой порции снега:
$ v_{n1-я}' = (\frac{M}{(M + m)})^{n} * v_{0}$;
2. Теперь рассмотрим тележку 2, на которой дворник спит. Найдём скорость тележки после падения первой порции снега:
$Mv_{0} = (M + m) v_{1}'$.
Скорость тележки стала:
$ v_{1}' = \frac{Mv_{0}}{M + m}$;
Скорость тележки 2 после падения второй порции снега:
$(M+m) *v_{1}' = (M + 2m) * v_{2}'$;
$v_{2}' = \frac{(M+m) *v_{1}' }{M + 2m} = \frac{M+m}{M + 2m} * \frac{Mv_{0}}{M + m} = \frac{Mv_{0}}{M + 2m}$;
Скорость тележки 2 после n−й порции снега:
$v_{n2-я}' = \frac{Mv_{0}}{M + nm}$;
3. Сравним выражения. Обозначим $x = \frac{m}{M}$. Тогда
$ v_{n1-я}' = \frac{v_{0}}{(1 + x)^{n}}$;
$v_{n2-я}' = \frac{v_{0}}{1 + nx}$;
Т.к. $(1 + x)^{n} > 1 + nx$, то $v_{n1-я}' < v_{n2-я}'$
Таким образом, быстрее будет двигаться тележка со спящим дворником, поэтому тележка 2 быстрее пройдёт заданное расстояние.
Приведенные вычисления показывают, что падающий на тележку снег замедляет ее импульс тем меньше, чем больше ее масса. Поэтому тележка, с которой снег не сбрасывают, движется быстрее.
Ответ: Быстрее пройдет тележка со спящим дворником.
Задание №1733
На одном конце доски массой М, находящейся на поверхности воды, сидит лягушка (рис. 270). С какой наименьшей скоростью должна прыгнуть лягушка, чтобы попасть в точку В? Расстояние между точками А и В равно l, масса лягушки m. Трение между доской и водой мало.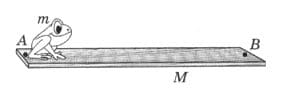 рис. 270
рис. 270
Решение
Дано:
M;
m;
l.
Найти:
v − ?
Решение: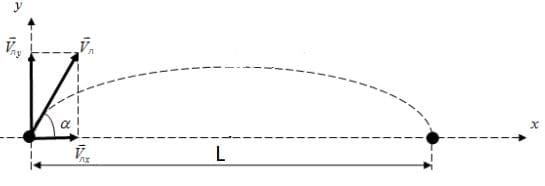 В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
В данной системе отсчета движение вдоль вертикальной оси Оy равноускоренное.
$v_{y} = v_{лy} + g_{y}t$;
Т.к. $v_{лy} = v_{л}sinα$; $g_{y} = -g$; $v_{y} = 0$, то
$0 = v_{л}sinα - gt$;
$v_{л}sinα = gt$;
$t = \frac{v_{л}sinα}{g}$;
Полное время полета лягушки равно:
$t = \frac{2v_{л}sinα}{g}$;
По закону сохранения импульса для системы «лягушка – доска»
$(m + M)v = mv_{л} + Mv_{д}$;
Так как v = 0, то в проекции на ось X уравнение примет вид:
$mv_{л}cosα - Mv_{д} = 0$;
$mv_{л}cosα = Mv_{д}$;
$v_{д} = \frac{mv_{л}cosα}{M}$;
За время полета лягушка должна преодолеть относительно доски расстояние l, равное:
$(v_{л}cosα + v_{д})t = l$;
$(v_{л}cosα + \frac{mv_{л}cosα}{M}) * \frac{2v_{л}sinα}{g} = l$;
$\frac{2v_{л}^{2}sinαcosα}{g} * ( 1+ \frac{m}{M}) = l$;
$v_{л}^{2}= \frac{l}{\frac{2sinαcosα}{g}* ( 1+ \frac{m}{M})} = \frac{l}{\frac{sin2α}{g}* ( 1+ \frac{m}{M})} = \frac{l}{\frac{sin2α}{g} + \frac{msin2α}{Mg}} = \frac{l}{\frac{sin2α *(M + m)}{gM}} = \frac{lgM}{sin2α * (M + m)}$;
$v_{л}= \sqrt{ \frac{lgM}{sin2α * (M + m)}}$;
Из формулы видно, что $v_{л}$ имеет минимальное значение при α = 45°.
Таким образом,
$v_{min}= \sqrt{ \frac{lgM}{M + m}}$.
Ответ: $\sqrt{ \frac{lgM}{M + m}}$.
Задание №1734
Тело массой 8 кг свободно падает с высоты 5 м. Рассчитайте потенциальную и кинетическую энергии этого тела на высоте 2 м от земли.
Решение
Дано:
m = 3 кг;
$v_{1} = 0$ м/с;
$h_{1} = 5$ м;
$h_{2} = 2$ м;
g = 10 Н/кг.
Найти:
$E_{п2}$ − ?
$E_{к2}$ − ?
Решение:
Найдем потенциальную энергию:
$E_{п2} = mgh_{2}$;
$E_{п2} = 3 * 10 * 2 = 60$ Дж;
Согласно закону сохранения механической энергии:
$E_{п1} + E_{к1} = E_{п2} + E_{к2}$;
$E_{к2} = E_{п1} + E_{к1} - E_{п2}$;
$E_{к} = \frac{mv^{2}}{2}$;
$E_{к2} = mgh_{1} + \frac{mv_{1}^{2}}{2} - E_{п2}$;
$E_{к2} = 3 * 10 * 5 + \frac{8 * 0^{2}}{2} - 60 = 90$ Дж.
Ответ: 60 Дж; 90 Дж.
Задание №1735
Мяч массой 200 г брошен под некоторым углом к горизонту со скоростью 10 м/с. Найдите потенциальную и кинетическую энергии мяча на высоте 4 м от земли.
Решение
Дано:
m = 200 г;
$v_{1} = 10$ м/с;
$h_{2} = 4$ м;
g = 10 Н/кг.
Найти:
$E_{п2}$ − ?
$E_{к2}$ − ?
СИ:
m = 0,2 кг.
Решение:
Полная механическая энергия мяча равна его начальной кинетической энергии:
$E_{к1} = \frac{mv_{1}^{2}}{2}$;
$E_{к1} = \frac{0,2 * 10^{2}}{2} = 10$ Дж;
На высоте 4 м от земли потенциальная энергия мяча равна:
$E_{п2} = mgh_{2}$;
$E_{п2} = 0,2 * 10 * 4 = 8$ Дж;
Согласно закону сохранения механической энергии:
$E_{п1} + E_{к1} = E_{п2} + E_{к2}$;
$E_{к2} = E_{п1} + E_{к1} - E_{п2}$;
$E_{к2} = 0 + 10 - 8 = 2$ Дж.
Ответ: 8 Дж; 2 Дж.
Задание №1736
Камень массой 2 кг, брошенный вертикально вверх со скоростью 20 м/с, упал на землю со скоростью 10 м/с. Рассчитайте изменение полной механической энергии камня.
Решение
Дано:
m = 2 кг;
$v_{1} = 20$ м/с;
$v_{2} = 10$ м/с;
g = 10 Н/кг.
Найти:
△E − ?
Решение:
Полная механическая энергия мяча в момент броска равна его начальной кинетической энергии:
$E_{к1} = \frac{mv_{1}^{2}}{2}$;
$E_{к1} = \frac{2* 20^{2}}{2} = 400$ Дж;
Полная механическая энергия мяча в момент падения равна его конечной кинетической энергии:
$E_{к2} = \frac{mv_{2}^{2}}{2}$;
$△E = E_{к2} - E_{к1} = \frac{mv_{2}^{2}}{2} - \frac{mv_{1}^{2}}{2} = \frac{m}{2} * (v_{2}^{2} - v_{1}^{2})$;
$△E = \frac{2}{2} * (10^{2} - 20^{2}) = 100 - 400 = -300$ Дж.
Ответ: − 300 Дж.
Задание №1737
Шайба массой 200 г, брошенная со скоростью 10 м/с вверх по ледяной горке, остановилась на высоте 3 м. На сколько изменилась полная механическая энергия шайбы?
Решение
Дано:
m = 200 г;
$v_{1} = 10$ м/с;
$h_{2} = 3$ м;
g = 10 Н/кг.
Найти:
△E − ?
СИ:
m = 0,2 кг.
Решение:
В начальной точке шайба обладает максимальной кинетической энергией и нулевой потенциальной. Полная механическая энергия равна:
$E_{1} = E_{к1} = \frac{mv_{1}^{2}}{2}$;
В верхней точке траектории скорость шайбы стала равна нулю. Поэтому её кинетическая энергия тоже стала равна нулю. Потенциальная энергия в этой точке возросла до максимума. Полная механическая энергия в конечной точке равна:
$E_{2} = E_{п_{2}} = mgh_{2}$;
Найдем изменение полной механической энергии:
$△E = E_{2} - E_{1} = mgh_{2} - \frac{mv_{1}^{2}}{2}$;
$△E = 0,2 * 10 * 3 - \frac{0,2 * 10^{2}}{2} = -4$ Дж.
Ответ: Уменьшилась на 4 Дж.

