Задание № 1111

Лампа имеет сопротивление 3 Ом. Чему равно сопротивление электрической цепи, состоящей из 6 таких ламп, соединённых параллельно? Чему равно сопротивление цепи, состоящей из 12 таких ламп?

Решение

Дано:
$R_{л} = 3$ Ом;
$N_{1}= 6$;
$N_{2} = 12$.
Найти:
$R_{1}$ − ?
$R_{2}$ − ?
Решение:
Сопротивление при параллельном соединении:
$R = \frac{R_{л}}{N}$;
$R_{1} = \frac{3}{6} = 0,5$ Ом;
$R_{1} = \frac{3}{12} = 0,25$ Ом.
Ответ: 0,5 Ом; 0,25 Ом.

Задание № 1112

Четыре одинаковых проводника, соединённых параллельно, имеют сопротивление 20 Ом. Чему равно сопротивление каждого из них?

Решение

Дано:
R = 20 Ом;
N = 4;
$R_{1} = R_{2} = R_{3} = R_{4}$.
Найти:
$R_{1}$ − ?
Решение:
Сопротивление при параллельном соединении:
$R = \frac{R_{1}}{N}$;
$R_{1} = N * R$;
$R_{1} = 4 * 20 = 80$ Ом.
$R_{1} = R_{2} = R_{3} = R_{4} = 80$ Ом.
Ответ: 80 Ом.

Задание № 1113

К проводнику сопротивлением 15 Ом подключили другой проводник, в результате чего сопротивление всего участка уменьшилось в 3 раза. Как подключили второй проводник − последовательно или параллельно? Чему равно сопротивление второго проводника?

Решение

Дано:
$R_{1} = 15$ Ом;
$R = \frac{R_{1}}{3}$.
Найти:
$R_{2}$ − ?
Решение:
Так как при подключении второго проводника сопротивление всего участка уменьшилось, то проводник подключили параллельно.
Сопротивление при параллельном соединении:
$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$;
$\frac{1}{R_{2}} = \frac{1}{R} - \frac{1}{R_{1}} = \frac{1}{\frac{R_{1}}{3}} - \frac{1}{R_{1}} = \frac{3}{R_{}1} - \frac{1}{R_{1}} = \frac{2}{R_{1}}$;
$R_{2} = \frac{R_{1}}{2}$;
$R_{2} = \frac{15}{2} = 7,5$ Ом.
Ответ: 7,5 Ом.

Задание № 1114

Рассчитайте, на сколько равных частей требуется разрезать проволоку из нихрома сопротивлением 1,6 Ом, чтобы при параллельном соединении отрезков получить сопротивление 0,1 Ом.

Решение

Дано:
$R_{н} = 1,6$ Ом;
$R_{к} = 0,1$ Ом.
Найти:
N − ?
Решение:
Сопротивление при последовательном соединении:
$R_{н} = R * N$;
$R = \frac{R_{н}}{N}$;
Сопротивление при параллельном соединении:
$R_{к} = \frac{R}{N} = \frac{ \frac{R_{н}}{N}}{N} = \frac{R_{н}}{N^{2}}$;
$N^{2} = \frac{R_{н}}{R_{к}}$;
$N = \sqrt{\frac{R_{н}}{R_{к}}}$;
$N = \sqrt{\frac{1,6}{0,1}} = \sqrt{16} = 4$.
Ответ: На 4 равные части.

Задание № 1115

Чему равно сопротивление участка цепи, изображённого на рисунке 172?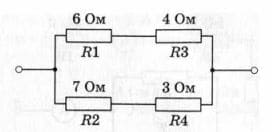
рис. 172

Решение

Дано:
$R_{1} = 6$ Ом;
$R_{2} = 7$ Ом;
$R_{3} = 4$ Ом;
$R_{4} = 3$ Ом.
Найти:
R − ?
Решение:
$R_{1}$ и $R_{3}$, $R_{2}$ и $R_{4}$ соединены последовательно.
$R_{13}$ и $R_{24}$ соединены параллельно.
При последовательном соединении:
$R_{13} = R_{1} + R_{3}$;
$R_{13} = 6 + 4 = 10$ Ом;
$R_{24} = R_{2} + R_{4}$;
$R_{24} = 7 + 3 = 10$ Ом;
При параллельном соединении:
R = $\frac{R_{13} * R_{24}}{R_{13} + R_{24}}$;
R = $\frac{10 * 10}{10 + 10} = 5$ Ом.
Ответ: 5 Ом.

Задание № 1116

Каким сопротивлением проводник следует включить параллельно прибору сопротивлением 12 Ом, чтобы получить сопротивление 4 Ом?

Решение

Дано:
$R_{1} = 12$ Ом;
R = 4 Ом.
Найти:
$R_{2}$ − ?
Решение:
При последовательном соединении:
$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$;
$\frac{1}{R_{2}} = \frac{1}{R} - \frac{1}{R_{1}}$;
$\frac{1}{R_{2}} = \frac{1}{4} - \frac{1}{12} = \frac{2}{12} = \frac{1}{6}$;
$R_{2} = 6$ Ом.
Ответ: 6 Ом.

Задание № 1117

Лампа накаливания и звонок соединены параллельно. Сопротивление лампы в 2 раза больше сопротивления звонка. Рассчитайте силу тока в лампе и звонке, если в неразветвлённой части цепи сила тока равна 0,6 А.

Решение

Дано:
$R_{2} = 2 R_{1}$
I = 0,6 А.
Найти:
$I_{1}$ − ?
$I_{2}$ − ?
Решение:
Сопротивление ри параллельном соединении:
$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} = \frac{1}{R_{1}} + \frac{1}{2 R_{1}} = \frac{3}{2R_{1}}$;
$R= \frac{2R_{1}}{3}$;
Найдем напряжение в цепи по закону Ома:
$U = IR = I * \frac{2R_{1}}{3} = 0,6 * \frac{2R_{1}}{3} = 0,4 R_{1}$;
При параллельном соединении напряжение равно:
$U = U_{1} = U_{2}$;
Найдем силу тока в лампе и звонке по закону Ома:
$I_{1} = \frac{U}{R_{1}} = \frac{0,4 R_{1}}{R_{1}} = 0,4$ А;
$I_{2} = \frac{U}{R_{2}} = \frac{0,4 R_{1}}{2R_{1}} = 0,2$ А.
Ответ: 0,4 А; 0,2 А.

Задание № 1118

Две лампы сопротивлением по 12 Ом каждая соединены параллельно и подключены к источнику тока напряжением 12 В. Чему равна сила тока в каждой лампе?

Решение

Дано:
$R_{1} = 12$ Ом;
N = 2 шт;
U = 12 В.
Найти:
$I_{1}$ − ?
$I_{2}$ − ?
Решение:
Сопротивление цепи при параллельном соединении:
$R = \frac{R_{1}}{n}$;
$R = \frac{12}{2} = 6$ Ом;
Найдем силу тока в цепи по закону Ома:
$I = \frac{U}{R}$;
$I = \frac{12}{6} = 2$ А;
Сила тока при параллельном соединении:
$I = N * I_{1}$;
$I_{1} = \frac{I}{N}$;
$I_{1} = \frac{2}{2} = 1$ А;
$I_{1} = I_{2} = 1$ А.
Ответ: 1 А; 1 А.

Задание № 1119

Два проводника сопротивлениями 5 и 10 Ом присоединены параллельно к источнику тока напряжением 20 В. Определите силу тока в каждом проводнике и в неразветвлённой части цепи. Начертите схему соединения проводников.

Решение

Дано:
$R_{1} = 5$ Ом;
$R_{2} = 10$ Ом;
U = 20 В.
Найти:
I − ?
$I_{1}$ − ?
$I_{2}$ − ?
Решение:
Напряжение в цепи и на концах всех параллельно соединённых проводников одно и то же:
$U = U_{1} = U_{2}$;
Найдем силу тока по закону Ома:
$I_{1} = \frac{U}{R_{1}} = \frac{20}{5} = 4$ А;
$I_{2} = \frac{U}{R_{2}} = \frac{20}{10} = 2$ А;
Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединённых проводниках:
$I = I_{1} + I_{2}$;
I = 4 + 2 = 6 А.
Ответ: 4 А; 2 А; 6 А.