Задание №1662

Во сколько раз скорость искусственного спутника, движущегося на высоте 21 600 км над поверхностью Земли, меньше скорости спутника, движущегося на высоте 600 км над поверхностью? Радиус Земли 6400 км.

Решение

Дано:
$h_{1} = 21 600$ км;
$h_{2} = 600$ км;
R = 6400 км.
Найти:
$\frac{v_{2}}{v_{1}}$ − ?
СИ:
$h_{1} = 21 600 000$ м;
$h_{2} = 600 000$ м;
R = 6 400 000 м.
Решение:
Первая космическая скорость равна:
$v = \sqrt{G * \frac{M_{з}}{R_{з} + h}}$;
$\frac{v_{2}}{v_{1}} = \frac{\sqrt{G * \frac{M_{з}}{R_{з} + h_{2}}}}{\sqrt{G * \frac{M_{з}}{R_{з} + h_{1}}}} = \sqrt {\frac{G * \frac{M_{з}}{R_{з} + h_{2}}}{G * \frac{M_{з}}{R_{з} + h_{1}}}} = \sqrt{\frac{R_{з} + h_{1}}{R_{з} + h_{2}}}$;
$\frac{v_{2}}{v_{1}} = \sqrt{\frac{6 400 000 + 21 600 000}{ 6 400 000 + 600 000}} = \sqrt{4} = 2$.
Ответ: В 2 раза.

Задание №1663

Сравните скорости движения искусственных спутников Земли и Венеры при движении по орбитам, одинаково удалённым от центров планет. Масса Венеры составляет 0,815 массы Земли.

Решение

Дано:
$r = R$;
m = 0,815M.
Найти:
$\frac{v_{2}}{v_{1}}$ − ?
СИ:
$h_{1} = 21 600 000$ м;
$h_{2} = 600 000$ м;
R = 6 400 000 м.
Решение:
Первая космическая скорость равна:
$v = \sqrt{G * \frac{M_{з}}{R}}$;
$\frac{v_{2}}{v_{1}} = \frac{\sqrt{G * \frac{M}{R}}}{\sqrt{G * \frac{m}{r}}} = \sqrt {\frac{G * \frac{M}{R}}{G * \frac{m}{r}}} = \sqrt {\frac{R * M}{R * 0,815M}} = \sqrt{1,227} = 1,11$.
Ответ: Скорость спутника Земли в 1,11 раза больше.

Задание №1664

Какую скорость должен иметь искусственный спутник Земли, чтобы он вращался по круговой орбите на высоте, равной двум радиусам Земли; трём радиусам Земли над поверхностью Земли? Радиус Земли равен 6400 км.

Решение

Дано:
$h_{1} = 2R$;
$h_{2} = 3R$;
R = 6400 км;
M = $6 * 10^{24}$ кг;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
$v_{1}$− ?
$v_{2}$− ?
СИ
R = 6 400 000 м.
Решение:
Первая космическая скорость равна:
$v_{1} = \sqrt{G * \frac{M_{з}}{R + h}} = \sqrt{G * \frac{M_{з}}{R + 2R}} = \sqrt{G * \frac{M_{з}}{3R}}$;
$v_{1} = \sqrt{6,67 * 10^{-11} * \frac{6 * 10^{24}}{3 * 6400 000}} = \sqrt{2,1 * 10^{7}} = 4583$ м/с ≈ 4,6 км/с;
$v_{2} = \sqrt{G * \frac{M_{з}}{R + h}} = \sqrt{G * \frac{M_{з}}{R + 3R}} = \sqrt{G * \frac{M_{з}}{4R}}$;
$v_{2} = \sqrt{6,67 * 10^{-11} * \frac{6 * 10^{24}}{4 * 6400 000}} = \sqrt{1,56 * 10^{7}} = 3950$ м/с ≈ 4 км/с.
Ответ: 4,6 км/с; 4 км/с.

Задание №1665

Может ли спутник обращаться вокруг Земли по круговой орбите со скоростью 1км/с? При каком условии это возможно?

Решение

Дано:
v = 1 км/с;
R = 6400 км;
M = $6 * 10^{24}$ кг;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
h − ?
СИ
$R = 0,64 * 10^{7}$ м;
v = 1000 м/с.
Решение:
Первая космическая скорость равна:
$v = \sqrt{G * \frac{M_{з}}{R + h}}$;
$v^{2}= G * \frac{M_{з}}{R + h}$;
$R + h= \frac{GM_{з}}{v^{2}}$;
$h = \frac{GM_{з}}{v^{2}} - R$;
$h = \frac{6,67 * 10^{-11} * 6 * 10^{24}}{1000^{2}} - 0,64 * 10^{7} = 40,02 * 10^{7} - 0,64 * 10^{7} = 39,38 * 10^{7} м ≈ 4 * 10^{8}$ м.
Ответ: Может при радиусе орбиты $4 * 10^{8}$ м.

Задание №1666

Радиус окружности, по которой движется Фобос (спутник планеты Марс), равен 9400 км, а его период обращения равен 46 мин. Определите массу Марса.

Решение

Дано:
R = 9400 км;
T = 46 мин;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
M − ?
СИ
$R = 9,4 * 10^{6}$ м;
T = 2760 с.
Решение:
Линейная скорость обращения спутника равна:
$v = \frac{2πR}{T}$;
Первая космическая скорость равна:
$v = \sqrt{G * \frac{M}{R}}$;
$v^{2}= G * \frac{М}{R}$;
$M = \frac{v^{2}R}{G} = \frac{(\frac{2πR}{T})^{2}R}{G} = \frac{4π^{2}R^{3}}{GT^{2}}$;
$M = \frac{4 * 3,14^{2} * (9,4 * 10^{6})^{3}}{6,67 * 10^{-11} * 2760^{2}} = 6,45 * 10^{25}$ кг.
Ответ: $6,45 * 10^{25}$ кг.

Задание №1667

Плотность некоторой планеты такая же, как и у Земли, а её радиус вдвое меньше. Найдите отношение первой космической скорости для Земли к аналогичной величине для некоторой планеты.

Решение

Дано:
$ρ_{п} = ρ_{з}$;
$R_{з} = 2R_{п}$.
Найти:
$\frac{v_{з}}{v_{п}}$ − ?
Решение:
Масса планеты равна:
$M = ρV = ρ * \frac{4}{3}πR^{3}$;
Первая космическая скорость равна:
$v = \sqrt{G * \frac{M}{R}} = \sqrt{G * \frac{ρ * \frac{4}{3}πR^{3}}{R}} = \sqrt{\frac{4GρπR^{3}}{3R}} = 2R\sqrt{\frac{Gρπ}{3}}$;
Найдем отношение скоростей:
$\frac{v_{з}}{v_{п}} = \frac{2R_{з}\sqrt{\frac{Gρ_{з}π}{3}}}{2R_{п}\sqrt{\frac{Gρ_{п}π}{3}}} = \frac{R_{з}}{R_{п}} = \frac{2R_{п}}{R_{п}} = 2$.
Ответ: 2.

Задание №1668

Рассчитайте скорость движения спутника вокруг Земли по круговой орбите на высоте, равной радиусу Земли, если первая космическая скорость у поверхности Земли равна 8 км/с.

Решение

Дано:
h = R;
$v_{1} = 8$ км/с;
R = 6400 км;
M = $6 * 10^{24}$ кг;
$G = 6,67 * 10^{-11} \frac{Н * м^{2}}{кг^{2}}$.
Найти:
v − ?
СИ
$v_{1} = 8000$ м/с;
R = 6400 000 м.
Решение:
Первая космическая скорость равна:
$v_{1} = \sqrt{G * \frac{M_{з}}{R}}$;
$v_{1}^{2} = G * \frac{M_{з}}{R}$;
$R = G * \frac{M_{з}}{v_{1}^{2}}$;
$v = \sqrt{G * \frac{M_{з}}{R+h}} = \sqrt{G * \frac{M_{з}}{R+R}} = \sqrt{G * \frac{M_{з}}{2R}} = \sqrt{G * \frac{M_{з}}{2 * G * \frac{M_{з}}{v_{1}^{2}}}} = \sqrt{\frac{v_{1}^{2}}{2}} = \frac{v_{1}}{\sqrt{2}}$;
$v = \frac{8000}{\sqrt{2}} = 5673$ м/ с ≈ 5,7 км/с.
Ответ: 5,7 км/с.

Задание №1669

Два спутника вращаются вокруг Земли по круговым орбитам на расстояниях 7600 и 600 км от её поверхности. Определите отношение скорости первого спутника к скорости второго.

Решение

Дано:
$h_{1} = 7600$ км;
$h_{2} = 600$ км;
R = 6400 км.
Найти:
$\frac{v_{1}}{v_{2}}$ − ?
СИ
$h_{1} = 7,6 * 10^{6}$ м;
$h_{2} = 6 * 10^{5}$ м;
$R = 6,4 * 10^{6}$ м.
Решение:
Первая космическая скорость равна:
$v_{1} = \sqrt{G * \frac{M_{з}}{R + h}}$;
$\frac{v_{1}}{v_{2}} = \frac{\sqrt{G * \frac{M_{з}}{R + h_{1}}}}{\sqrt{G * \frac{M_{з}}{R + h_{2}}}} = \sqrt{\frac{\frac{G * M_{з}}{R + h_{1}}}{\frac{G * M_{з}}{R + h_{2}}}} = \sqrt{\frac{R + h_{2}}{R + h_{1}}}$;
$\frac{v_{1}}{v_{2}} = \sqrt{\frac{6,4 * 10^{6} + 6 * 10^{5}}{6,4 * 10^{6} + 7,6 * 10^{6}}} = \sqrt{0,5} = 0,7$.
Ответ: 0,7.

Задание №1670

На рисунке 255 показаны силы, действующие на тело, движущееся по окружности ($\overset{→}{N}$ − сила реакции опоры; $\overset{→}{F_{н}}$ сила натяжения нити). Запишите уравнение движения тела в векторной и скалярной формах для каждого случая.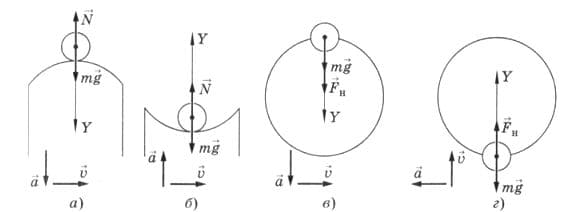
рис. 255

Решение

а) Уравнение движения тела в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N}$;
Проекция на ось Y:
ma = mg − N;
$\frac{mv^{2}}{R} = mg - N$.

б) Уравнение движения тела в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{N}$;
Проекция на ось Y:
ma = N − mg;
$\frac{mv^{2}}{R} = N - mg$.

в) Уравнение движения тела в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{F_{н}}$;
Проекция на ось Y:
$ma = mg + F_{н}$;
$\frac{mv^{2}}{R} = mg + F_{н}$.

г) Уравнение движения тела в векторной форме:
$\overset{→}{mа} = \overset{→}{mg} + \overset{→}{F_{н}}$;
Проекция на ось Y:
$0 = F_{н} - mg$;
Проекция на ось X:
ma = 0.

Задание №1671

Анализируя движение тел по наклонной плоскости − спуск и подъём (рис. 256), Галилей пришёл к выводу, что движение тела по горизонтальной плоскости является равномерным. Как рассуждал учёный?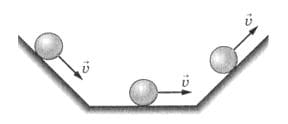
рис. 256

Решение

"При движении по наклонной плоскости вниз наблюдается ускорение, а при движении вверх − замедление. Отсюда следует, что движение по горизонтали является неизменным, ибо... оно ничем не ослабляется, не замедляется и не ускоряется".