Задание №1644

Определите направление и модуль скорости, а также ускорение в точках А, В, С, D (рис. 253) колеса автомобиля, движущегося с постоянной скоростью $v_{0} = 20$ м/с, если радиус колеса равен 0,5 м.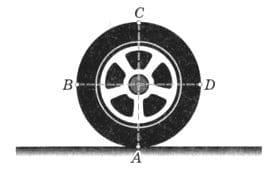
рис. 253

Решение

Найдем скорость движения точек обода колеса в системе отсчёта, связанной с автомобилем.
Дано:
R = 0,5 м;
$v_{0} = 20$ м/с.
Найти:
v − ?
$a_{ц}$ − ?
Решение:
Найдем путь, который пройдет колесо за период его вращения:
S = 2πR;
Время, за которое будет пройден путь, равный длине окружности колеса − это период его вращения:
$t = T = \frac{S}{v_{0}} = \frac{2πR}{v_{0}}$;
Найдем скорость точек колеса относительно оси его вращения.
$v = \frac{2πR}{T} = \frac{2πR}{\frac{2πR}{v_{0}}} = v_{0}$;
v = 20 м/с.
$a_{ц} = \frac{v^{2}}{R}$;
$a_{ц} = \frac{20^{2}}{0,5} = 800 м/с^{2}$.
Ответ: 20 м/с; $800 м/с^{2}$.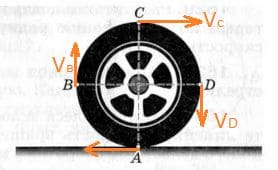

Задание №1645

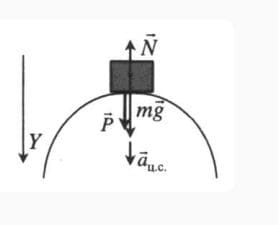
Гонщик на трассе соревнований после спуска автомобиля по склону горы испытал в точке А состояние невесомости (рис. 254). Радиус закругления трассы в данном месте равен 25 м. Чему равна скорость автомобиля в точке А? Какое состояние испытал гонщик в точке В?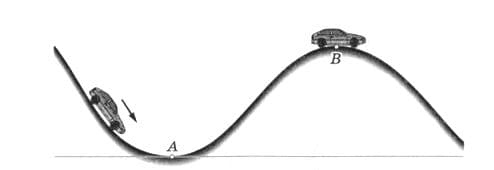

Решение
Дано:
P = 0;
R = 25 м.
Найти:
v − ?
Решение:
Т.к. автомобиль движется криволинейно, то ускорение в т. А направлено к центру окружности, т. е. вверх. В т. А на автомобиль действуют сила тяжести и сила реакции опоры. Согласно второму закону Ньютона:
$a_{ц} = \frac{F}{m} = \frac{N - F_{т}}{m} = \frac{N - mg}{m} $;
$ma_{ц} = N - mg$;
$N = ma_{ц} + mg$;
По третьему закону вес равен по модулю силе реакции опоры:
$N = P = ma_{ц} + mg = 0$;
$mg = |ma_{ц}|$;
$g = a_{ц}$;
То есть гонщик окажется в состоянии невесомости, если центростремительное ускорение, возникающее при движении на трассе, будет равно модулю ускорения свободного падения:
Центростремительное ускорение равно:
$a_{ц} = \frac{v^{2}}{R}$;
$v^{2} = a_{ц} * R$;
$v = \sqrt{a_{ц} * R} = \sqrt{g* R}$;
$v = \sqrt{10 * 25} = 15,8$ м/с.
Ответ: 15,8 м/с.

В точке B гонщик также испытал состояние невесомости.

Задание №1646

Лётчик массой 80 кг совершает петлю Нестерова радиусом 250 м. При этом скорость самолёта 540 км/ч. С какой силой давит лётчик на сиденье кресла в нижней точке петли?

Решение

Дано:
m = 80 кг;
R = 250 м;
v = 540 км/ч;
g ≈ 10 $м/с^{2}$.
Найти:
P − ?
СИ:
v = 150 м/с.
Решение:
Т.к. самолет движется по окружности, то центростремительное ускорение в нижней точке петли направлено к центру окружности, т. е. вверх:
$a_{ц} = \frac{v^{2}}{R}$;
В нижней точки петли на самолет действуют сила тяжести и сила реакции опоры. Согласно второму закону Ньютона:
$ma_{ц} = N - mg$;
$N = ma_{ц} + mg$;
По третьему закону вес равен по модулю силе реакции опоры:
$N = P = ma_{ц} + mg = m * ( \frac{v^{2}}{R} + g)$;
$F = 80 * ( \frac{150^{2}}{250} + 10) = 8000$ Н = 8 кН.
Ответ: 8 кН.

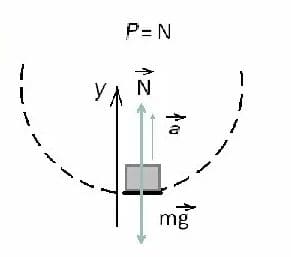
Задание №1647

Самолёт выходит из пикирования, описывая в вертикальной плоскости дугу окружности радиусом 800 м, имея скорость в нижней точке 200 м/с. Какую перегрузку испытывает лётчик в нижней точке траектории?

Решение

Дано:
R = 800 м;
v = 200 м/с.
Найти:
$\frac{△P}{P}$ − ?
Решение:
Центростремительное ускорение в нижней точки дуги равно:
$a_{ц} = \frac{v^{2}}{R}$;
По второму закону Ньютона найдем изменение веса парашютиста:
F = mg;
$ma_{ц} = N - mg$;
$N = ma_{ц} + mg$;
По третьему закону вес равен по модулю силе реакции опоры:
$N = △P = ma_{ц} + mg = m * (a_{ц} + g)$;
$\frac{△P}{P} = \frac{m * (a_{ц} + g)}{mg} = \frac{a_{ц}}{g} + 1 = \frac{\frac{v^{2}}{R}}{g} + 1 = \frac{v^{2}}{Rg} + 1$;
$\frac{△P}{P} = \frac{200^{2}}{800 * 10} + 1 = 6$.
Ответ: 6.

Задание №1648

С какой скоростью должен проходить автомобиль середину выпуклого моста радиусом 40 м, чтобы пассажир на мгновение оказался в состоянии невесомости?

Решение

Дано:
P = 0;
R = 40 м.
Найти:
v − ?
Решение:
Т.к. автомобиль движется криволинейно, то ускорение в т. А направлено к центру окружности, т. е. вниз. На автомобиль действуют сила тяжести и сила реакции опоры. Согласно второму закону Ньютона:
$ma_{ц} = mg - N$;
$N = mg - ma_{ц}$;
По третьему закону вес равен по модулю силе реакции опоры:
$N = P = mg - ma_{ц} = 0$;
$mg = ma_{ц}$;
$g = a_{ц}$;
То есть пассажир окажется в состоянии невесомости, если центростремительное ускорение, возникающее при движении по мосту, будет равно ускорению свободного падения:
Центростремительное ускорение равно:
$a_{ц} = \frac{v^{2}}{R}$;
$v^{2} = a_{ц} * R$;
$v = \sqrt{a_{ц} * R} = \sqrt{g* R}$;
$v = \sqrt{10 * 40} = 20$ м/с.
Ответ: 20 м/с.

Задание №1649

Приведите во вращение в вертикальной плоскости шарик на нити. С помощью секундомера и рулетки определите период и частоту обращения, угловую скорость, линейную скорость, ускорение шарика.

Решение

Оборудование: секундомер, рулетка.
Ход работы:
1. Приведем во вращение в вертикальной плоскости шарик на нити.
2. С помощью секундомера определим за какое время шарик сделал 10 оборотов. Допустим шарик сделал 10 оборотов (N) за 8 сек. (t).
3. Найдем период обращения шарика.
$T = \frac{t}{N} = \frac{8}{10} = 0,8$ с.
4. Найдем частоту обращения шарика.
$ν = \frac{N}{t} = \frac{10}{8} = 1,25 с^{-1}$.
5. Измерим длину нити, к которой прикреплен шарик. Допустим длина нити равна 0,15 м (R).
6. Найдем линейную скорость движения шарика.
$v = \frac{2πR}{T} = \frac{2 * 3,14 * 0,15}{0,8} = 1,18$ м/с.
7. Найдем угловую скорость движения шарика.
$v = \frac{2π}{T} = \frac{2 * 3,14}{0,8} = 7,85$ м/с.
8. Найдем ускорение шарика.
$a_{ц} = \frac{v^{2}}{R} =\frac{1,18^{2}}{0,15} = 9,3 м/с^{2}$.