Задание №1489

Парашютист весом 800 Н спускается с раскрытым парашютом. Чему равна сила сопротивления воздуха при равномерном движении парашютиста? Чему равна равнодействующая сила в этом случае? Решите задачу графически.

Решение

Парашютист спускается равномерно, значит равнодействующая всех сил, приложенных к нему, равна нулю.
Вес парашютиста, направленный вертикально вниз, равен 800 Н, значит сила сопротивления воздуха, направленная в противоположенную сторону движения, то есть вертикально вверх, равна ему по модулю и составляет 800 Н.

Задание №1490

Сложите графически две силы 50 и 30 Н, направленные друг к другу под углом 0°; 180°.

Решение

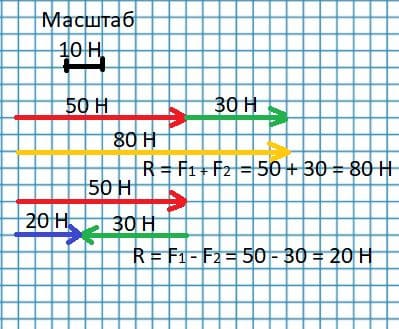Ответ: 80 Н; 20 Н.

Задание №1491

В каких случаях две силы 4 и З Н, приложенные к одной точке, имеют равнодействующую, равную 7, 1, 5 Н?

Решение

1.Если две силы 4 и З Н действуют вдоль одной прямой и направлены в одну сторону, то их равнодействующая равна:
$R = F_{1} + F_{2} = 4 + 3 = 7$ Н.
2.Если две силы 4 и З Н действуют вдоль одной прямой и направлены в противоположные стороны, то их равнодействующая равна:
$R = F_{1} + F_{2} = 4 - 3 = 1$ Н.
3.Если две силы 4 и З Н направлены перпендикулярно друг другу, то по теореме Пифагора их равнодействующая равна:
$R = \sqrt{F_{1}^{2} + F_{2}^{2}} = \sqrt{4^{2} + 3^{2}} = 5$ Н.

Задание №1492

Деталь закреплена в трёхкулачковом патроне. Чему равна равнодействующая сила, если каждый кулачок действует силой F, а расположены они под углом 120° друг к другу?

Решение

Дано:
$F_{1} = F_{2} = F_{3}$;
∠ = 120°;
Найти:
F − ?
Решение: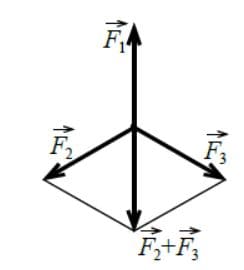
Сложим $\overset{→}{F_{2}}$ и $\overset{→}{F_{3}}$ по правилу параллелограмма. Вследствие равенства модулей сил $\overset{→}{F_{2}}$ и $\overset{→}{F_{3}}$ этот параллелограмм есть ромб. Сумма сил $\overset{→}{F_{2}} + \overset{→}{F_{3}}$ есть диагональ ромба, поэтому углы между парами векторов $\overset{→}{F_{2}}$ и $\overset{→}{F_{2}} + \overset{→}{F_{3}}$, а также $\overset{→}{F_{3}}$ и $\overset{→}{F_{2}} + \overset{→}{F_{3}}$ равны по 60°, т. е. векторы $\overset{→}{F_{1}}$ и $\overset{→}{F_{2}} + \overset{→}{F_{3}}$ направлены вдоль одной прямой, но в противоположные стороны. Силовой параллелограмм, построенный на векторах $\overset{→}{F_{2}}$ и $\overset{→}{F_{3}}$, состоит из двух равносторонних треугольников, поэтому модуль силы
$|\overset{→}{F_{2}} + \overset{→}{F_{3}}| = F_{2} = F_{3} = F_{1}$, т. е $\overset{→}{F_{1}} = - (\overset{→}{F_{2}} + \overset{→}{F_{3}})$,
откуда следует $\overset{→}{F_{1}} + \overset{→}{F_{2}} + \overset{→}{F_{3}} = 0$.
Ответ: 0

Задание №1493

С каким ускорением двигался при разгоне реактивный самолёт массой 60 т, если сила тяги двигателей 90 кН? Сопротивление воздуха не учитывать.

Решение

Дано:
m = 60 т;
F = 90 кН.
Найти:
а − ?
СИ:
m = 60 000 кг;
F = 90 000 Н.
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
$a = \frac{90000}{60000} = 1,5 м/с^{2}$.
Ответ: 1,5 $м/с^{2}$.

Задание №1494

Один из реактивных снарядов установки «Катюша» периода Великой Отечественной войны имел массу 42,5 кг и запускался реактивной силой 19,6 кН. Какое ускорение он получал при этом?

Решение

Дано:
m = 42,5 кг;
F = 19,6 кН.
Найти:
а − ?
СИ:
F = 19 600 Н.
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
$a = \frac{19600}{42,5} = 461 м/с^{2}$.
Ответ: 461 $м/с^{2}$.

Задание №1495

Определите массу автомобиля, движущегося при торможении с ускорением 2 $м/с^{2}$, если сила трения равна 6 кН.

Решение

Дано:
a = 2 $м/с^{2}$;
F = 6 кН.
Найти:
m − ?
СИ:
F = 6 000 Н.
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
$m = \frac{F}{a}$;
$m = \frac{6000}{2} = 3000$ кг.
Ответ: 3000 кг.

Задание №1496

Рассчитайте силу, сообщающую вагонетке массой 200 кг ускорение 0,2 $м/с^{2}$.

Решение

Дано:
a = 0,2 $м/с^{2}$;
m = 200 кг.
Найти:
F − ?
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
F = am;
F = 0,2 * 200 = 40 Н.
Ответ: 40 Н.

Задание №1497

Под действием некоторой силы тело массой 10 кг приобрело ускорение 2 $м/с^{2}$. Какое ускорение приобретёт тело массой 5 кг под действием такой же силы?

Решение

Дано:
$a_{1} = 2 м/с^{2}$;
$m_{1} = 10$ кг;
$m_{2} = 5$ кг;
$F_{1} = F_{2}$.
Найти:
$a_{2}$ − ?
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
F = am;
Так как $F_{1} = F_{2}$, то
$a_{1}m_{1} = a_{2}m_{2}$;
$a_{2} = \frac{a_{1}m_{1}}{m_{2}}$;
$a_{2} = \frac{2 * 10}{5} = 4 м/с^{2}$.
Ответ: 4 $м/с^{2}$.

Задание №1498

Сила 40 Н сообщает телу ускорение 0,8 $м/с^{2}$. Какую силу надо приложить, чтобы сообщить этому телу ускорение 1,6 $м/с^{2}$?

Решение

Дано:
$F_{1} = 40$ Н.
$a_{1} = 0,8 м/с^{2}$;
$a_{2} = 1,6 м/с^{2}$;
$m_{1} = m_{2}$.
Найти:
$F_{2}$ − ?
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
$m = \frac{F}{a}$;
Так как $m_{1} = m_{2}$, то
$\frac{F_{1}}{a_{1}} = \frac{F_{2}}{a_{2}}$;
$F_{2} = \frac{F_{1} *a_{2}}{a_{1}}$;
$F_{2} = \frac{40 * 1,6}{0,8} = 80$ Н.
Ответ: 80 Н.

Задание №1499

Порожний грузовой автомобиль массой 3 т начал движение с ускорением 0,2 $м/с^{2}$. Чему равна масса автомобиля вместе с грузом, если при той же силе тяги он трогается с места с ускорением 0,15 $м/с^{2}$?

Решение

Дано:
$m_{1} = 3$ т;
$a_{1} = 0,2 м/с^{2}$;
$a_{2} = 0,15 м/с^{2}$;
$F_{1} = F_{2}$.
Найти:
$m_{2}$ − ?
СИ:
$m_{1} = 3 000$ кг.
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
F = am;
Так как $F_{1} = F_{2}$, то
$a_{1}m_{1} = a_{2}m_{2}$;
$m_{2} = \frac{a_{1}m_{1}}{a_{2}}$;
$m_{2} = \frac{0,2 *3000}{0,15} = 4000$ кг = 4 т.
Ответ: 4 т.

Задание №1500

Пуля массой 7,9 г вылетает под действием пороховых газов из канала ствола длиной 45 см со скоростью 700 м/с. Вычислите среднюю силу давления пороховых газов. Трением пули о стенки ствола пренебречь.

Решение

Дано:
m = 7,9 г;
S = 45 см;
v = 700 м/с.
Найти:
F − ?
СИ:
m = 0,0079 кг;
S = 0,45 м.
Решение:
Уравнение скорости:
$v = v_{0} + at$;
Пуля начинает движение, поэтому $v_{0} = 0$ м/с.
v = at;
$t = \frac{v}{a}$;
Уравнение движения:
$S = v_{0}t + \frac {at^{2}}{2}$;
Так как $v_{0} = 0$, то
$S = \frac {at^{2}}{2} = \frac {a * ( \frac{v}{a})^{2}}{2} = \frac {v^{2}}{2a}$;
$a = \frac {v^{2}}{2S}$;
$a = \frac {700^{2}}{2 * 0,45} = 544 444 м/с^{2}$;
По второму закону Ньютона:
$a = \frac{F}{m}$;
F = am;
F = 544 444 * 0,0079 = 4301 Н ≈ 4,3 кН.
Ответ: 4,3 кН.

Задание №1501

Столкнулись две тележки. При этом тележка массой 0,5 кг получила ускорение 4 $м/с^{2}$. Какое ускорение получила тележка массой 0,8 кг?

Решение

Дано:
$m_{1} = 0,5$ кг;
$a_{1} = 4 м/с^{2}$;
$m_{2} = 0,8$ кг;
$F_{1} = F_{2}$.
Найти:
$a_{2}$ − ?
Решение:
По второму закону Ньютона:
$a = \frac{F}{m}$;
F = am;
Так как $F_{1} = F_{2}$, то
$a_{1}m_{1} = a_{2}m_{2}$;
$a_{2} = \frac{a_{1}m_{1}}{m_{2}}$;
$a_{2} = \frac{4 * 0,5}{0,8} = 2,5 м/с^{2}$.
Ответ: 2,5 $м/с^{2}$.