Задание №1453

По графикам зависимости скорости от времени (рис. 236) определите, какое из четырёх тел прошло наибольший путь за интервал времени от $t_{1} = 0$ до $t_{2} = 3$ c.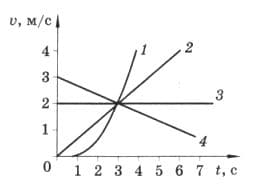
рис. 236

Решение

Путь численно равен площади фигуры, заключённой под графиком зависимости скорости от времени.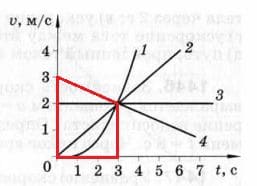
Под графиком скорости 1−го тела находится криволинейный треугольник.
Под графиком скорости 2−го тела находится треугольник
Под графиком скорости 3−го тела находится прямоугольник.
Под графиком скорости 4−го тела находится трапеция, которая состоит из вышеназванных фигур.
Значит четвёртое тело прошло наибольший путь за интервал времени от $t_{1} = 0$ до $t_{2} = 3$ c

Задание №1454

Проанализируйте графики, приведённые на рисунке 237. Есть ли между ними какая − либо связь?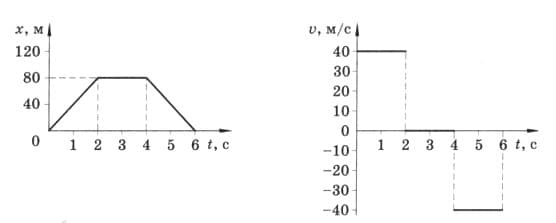
рис. 237

Решение

На участке 0 − 2 с тело двигалось равномерно, затем 2 с покоилось, а последние 2 с двигалось с прежней скоростью в обратном направлении и вернулось к месту начала движения.
График v (t) полностью соответствует описанному движению: участок 0 − 2 с: v = 40 м/с; участок 2 − 4 с: v = 0; участок 4 − 6 с: v = − 40 м/с.
Эти графики показывают движение одного и того же тела. Первый график показывает зависимость координаты от времени, второй график − зависимость скорости от времени.

Задание №1455

По графикам, приведённым на рисунке 238, определите ускорение. Чем различаются эти движения?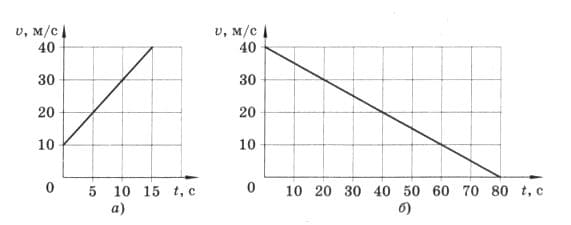
рис. 238

Решение

а) Из графика следует, что $v_{0} = 10$ м/с, v = 40 м/с; t = 15 с.
Найдем ускорение тела:
$v = v_{0} + at$;
$at = v - v_{0}$;
$a = \frac{v - v_{0}}{t}$;
$a = \frac{40 - 10}{15} = 2м/с^{2}$.

б) Из графика следует, что $v_{0} = 40$ м/с, v = 0; t = 80 с.
Найдем ускорение тела:
$a = \frac{v - v_{0}}{t}$;
$a = \frac{0 - 40}{80} = - 0,5м/с^{2}$.

в) На графике а) − прямолинейное равноускоренное движение, a > 0,
на графике б) − прямолинейное равнозамедленое движение, a < 0.

Задание №1456

По графику ускорения частицы (рис. 239) постройте график зависимости её скорости от времени. Начальную скорость частицы принять равной нулю.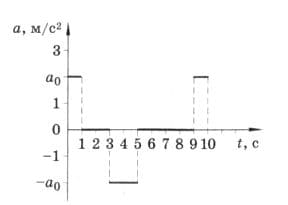
рис. 239

Решение

Уравнение скорости движения:
$v = v_{0} + at$.
В 1−ю секунду движения разгон с ускорением a = 2 $м/с^{2}$; $v_{0} = 0$ м/с; v = 2 * 1 = 2 м/с.
Во 2−ю и 3−ю секунды − равномерное движение: a = 0; v = 2 м/с.
В 4−ю секунду движения тело двигалось до остановки с ускорением a = −2 $м/с^{2}$; $v_{0} = 2$ м/с; v = 2 − 2 * 1 = 0 м/с.
В 5−ю секунды движения разгон против оси Х с ускорением a = −2 $м/с^{2}$; $v_{0} = 0$ м/с; v = 0 − 2 * 1 = −2 м/с.
С 6−й по 9−ю секунды − равномерное движение: a = 0; v = −2 м/с.
В 10−ю секунду движения торможение до остановки с ускорением a = 2 $м/с^{2}$; $v_{0} = -2$ м/с; v = −2 + 2 * 1 = 0 м/с.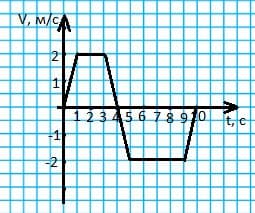

Задание №1457

По графику зависимости скорости движения тела от времени (рис. 240) найдите:
а) путь, пройденный телом за 2 с; 4 с;
б) координату тела в момент времени t = 4 с;
в) ускорение движения тела.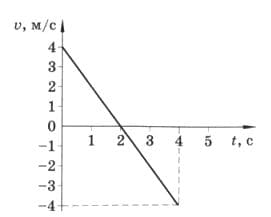
рис. 240

Решение

а) Путь можно определить либо аналитически, либо графически (как площадь соответствующего треугольника).
Из графика следует, что $v_{0} = 4$ м/с, v = 0; t = 2 c;
$S = \frac {v_{0} + v}{2} * t$;
$S_{1} = \frac {4 + 0}{2} * 2 = 4$ м.
Остальные 2 секунды тело движется в направлении, противоположном направлению оси координат в выбранной системе отсчета. $v_{0} = 0$ м/ с; v = −4 м/с; t = 2 с.
$|S_{2}| = |\frac {0-4}{2} * 2| = 4$ м.
$S = S_{1} + S_{2} = 4 + 4 = 8$ м.
Ответ: 4 м; 8 м.

б) Найдем ускорение тела:
$v = v_{0} + at$;
$v - v_{0} = at$;
$a = \frac{v - v_{0}}{t}$;
$|a| = |\frac{0 - 4}{2}| = 2 м/с^{2}$.
Ответ: 2 $м/с^{2}$.

в) х = 0, так как тело 2 с двигалось с ускорением а = −2 $м/с^{2}$ до остановки (v = 0), а затем с ускорением а = 2 $м/с^{2}$ двигалось в противоположную сторону тоже 2 с, т. е. оно вернулось в первоначальное положение.
Ответ: x = 0.