Задание № 1165

Сила тока в спирали электроплитки мощностью 600 Вт равна 5 А. Чему равно сопротивление спирали?

Решение

Дано:
I = 5 А;
P = 600 Вт.
Найти:
R − ?
Решение:
P = UI;
$U = \frac{P}{I}$;
$R = \frac{U}{I} = \frac{\frac{P}{I}}{I} = \frac{P}{I^{2}}$;
$R = \frac{600}{5^{2}} = 24$ Ом.
Ответ: 24 Ом.

Задание № 1166

Рассчитайте сопротивление ламп мощностью 25, 40, 60 и 100 Вт, рассчитанных на напряжение 220 В.

Решение

Дано:
$P_{1} = 25$ Вт;
$P_{2} = 40$ Вт;
$P_{3} = 60$ Вт;
$P_{4} = 100$ Вт;
U = 220 В.
Найти:
$R_{1}$ − ?
$R_{2}$ − ?
$R_{3}$ − ?
$R_{4}$ − ?
Решение:
P = UI;
$I = \frac{P}{U}$;
$R = \frac{U}{I} = \frac{U}{\frac{P}{U}} = \frac{U^{2}}{P}$;
$R_{1} = \frac{U^{2}}{P_{1}} = \frac{220^{2}}{25} = 1936$ Ом;
$R_{2} = \frac{U^{2}}{P_{2}} = \frac{220^{2}}{40} = 1210$ Ом;
$R_{3} = \frac{U^{2}}{P_{3}} = \frac{220^{2}}{60} = 807$ Ом;
$R_{4} = \frac{U^{2}}{P_{4}} = \frac{220^{2}}{100} = 484$ Ом.
Ответ: 1936 Ом; 1210 Ом; 807 Ом; 484 Ом.

Задание № 1167

Предохранители в квартире рассчитаны на силу тока 6 А. Можно ли включить в сеть электроутюг мощностью 800 Вт, если уже включены четыре лампы мощностью по 100 Вт каждая? Напряжение в сети 220 В.

Решение

Дано:
I = 6 А;
$P_{1} = 800$ Вт;
$P_{2} = 100$ Вт;
$n_{2} = 4$ шт.;
U = 220 В.
Найти:
$I > I_{расч}$ − ?
Решение:
Найдем мощность при использовании всех электроприборов:
$P = P_{1} + n_{2} * P_{2}$;
P = 800 + 4 * 100 = 1200 Вт;
Найдем силу тока:
$I_{расч} = \frac{P}{U}$;
$I_{расч} = \frac{1200}{220} = 5,45$ А;
$I > I_{расч}$. Расчетный ток потребителей ниже чем ток срабатывания предохранителей. Утюг включить можно.
Ответ: Утюг включить можно.

Задание № 1168

Лампа накаливания мощностью 100 Вт включена в сеть напряжением 220В. Найдите сопротивление нити лампы в режиме горения, силу тока в лампе и месячный расход энергии при условии, что в день лампа горит в течение 5 ч. Количество дней в месяце считать равным 30.

Решение

Дано:
P = 100 Вт;
U = 220 В;
$t_{1} = 5$ ч;
n = 30 дней.
Найти:
R − ?
I − ?
$А_{мес}$ − ?
Решение:
Найдем силу тока в лампе:
P = UI;
$I = \frac{P}{U}$;
$I = \frac{100}{220} = 0,45$ А;
Надем сопротивление нити лампы по закону Ома:
$R = \frac{U}{I}$;
$R = \frac{220}{0,45} = 484$ Ом;
Найдем месячный расход энергии:
$t_{мес}= nt_{1}$;
$A = UIt_{мес} = UI * nt_{1}$;
A = 220 * 0,45 * 30 * 5 = 14 850 Вт * ч ≈ 15 кВт * ч.
Ответ: 0,45 А; 484 Ом; 15 кВт * ч.

№1169

По рисунку 179 определите мощность тока, потребляемую лампой $Л_{2}$.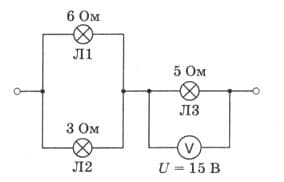
рис. 179

Решение

Дано:
$R_{1} = 6$ Ом;
$R_{2} = 3$ Ом;
$R_{3} = 5$ Ом;
$U_{3} = 15$ В.
Найти:
$P_{2}$ − ?
Решение:
Лампы $Л_{1}$ и $Л_{2}$ соединены параллельно, лампы $Л_{12}$ и $Л_{3}$ соединены последовательно.
Найдем силу тока по закону Ома:
$I_{3} = \frac{U_{3}}{R_{3}}$;
$I_{3} = \frac{15}{5} = 3$ А.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
$I_{3} = I_{12} = I = 3$ А;
Найдем общее сопротивление ламп $Л_{1}$ и $Л_{2}$:
$R_{12} = \frac{R_{1} * R_{2}}{R_{1} + R_{2}}$;
$R_{12} = \frac{6 * 3}{6 + 3} = 12$ Ом;
Найдем напряжение по закону Ома:
$U_{12} = I_{12} * R_{12}$;
$U_{12} = 3 * 12 = 36$ В;
Напряжение на участке цепи и на концах всех параллельно соединённых проводников одинаково:
$U_{12} = U_{1} = U_{2} = 36$ В;
Найдем мощность лампы $Л_{2}$:
$I_{2} = \frac{U_{2}}{R_{2}}$;
$P_{2} = U_{2}I_{2} = \frac{U_{2}^{2}}{R_{2}}$;
$P_{2} = \frac{36}{3} = 12$ Вт.
Ответ: 12 Вт.

Задание № 1170

По рисунку 180 найдите мощность тока, потребляемую лампой $Л_{1}$.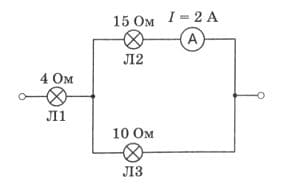
рис. 180

Решение

Дано:
$R_{1} = 4$ Ом;
$R_{2} = 15$ Ом;
$R_{3} = 10$ Ом;
$I_{2} = 2$ А.
Найти:
$P_{1}$ − ?
Решение:
Лампы $Л_{2}$ и $Л_{3}$ соединены параллельно, лампы $Л_{1}$ и $Л_{23}$ соединены последовательно.
Найдем напряжение тока по закону Ома:
$U_{2} = I_{2}R_{2}$;
$U_{2} = 2 * 15 = 30$ В;
Напряжение на участке цепи и на концах всех параллельно соединённых проводников одинаково:
$U_{2} = U_{3} = U_{23} = 30$ В;
Найдем общее сопротивление ламп $Л_{2}$ и $Л_{3}$:
$R_{23} = \frac{R_{2} * R_{3}}{R_{2} + R_{3}}$;
$R_{23} = \frac{15 * 10}{15 + 10} = 6$ Ом;
Найдем силу тока по закону Ома:
$I_{23} = \frac{U_{23}}{R_{23}}$;
$I_{23} = \frac{30}{6} = 5$ А.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
$I_{1} = I_{23} = 5$ А;
Найдем мощность лампы $Л_{1}$:
$U_{1} = I_{1}R_{1}$;
$P_{1} = U_{1}I_{1} = I_{1}^{2}R_{1}$;
$P_{1} = 5^{2} * 4 = 100$ Вт.
Ответ: 100 Вт.

Задание № 1171

Спираль изготовлена из фехралевого провода площадью поперечного сечения 0,5 $мм^{2}$ и длиной 4 м. Чему равна потребляемая мощность тока, если спираль включена в сеть напряжением 120 В?

Решение

Дано:
S = 0,5 $мм^{2}$;
l = 4 м;
U = 120 В;
$ρ = 1,2 \frac{Ом * мм^{2}}{м}$.
Найти:
P − ?
Решение:
Найдем сопротивление спирали:
$R = \frac{ρl}{S}$;
$R = \frac{1,2 * 4}{0,5} = 9,6$ Ом;
Найдем мощность тока:
$I = \frac{U}{R}$;
P = UI = $\frac{U^{2}}{R}$;
P = $\frac{120^{2}}{9,6} = 1500$ Вт = 1,5 кВт.
Ответ: 1,5 кВт.

Задание № 1172

Имеется нихромовая проволока площадью поперечного сечения 0,2 $мм^{2}$. Сколько метров проволоки потребуется для намотки паяльника мощностью 100 Вт, рассчитанного на напряжение 120 В?

Решение

Дано:
S = 0,2 $мм^{2}$;
P = 100 Вт;
U = 120 В;
$ρ = 1,1 \frac{Ом * мм^{2}}{м}$.
Найти:
l − ?
Решение:
Найдем сопротивление проволоки:
$I = \frac{U}{R}$;
$P = UI = \frac{U^{2}}{R}$;
$R = \frac{U^{2}}{P}$;
$R = \frac{120^{2}}{100} = 144$ Ом;
Найдем длину проволоки:
$R = \frac{ρl}{S}$;
$l = \frac{RS}{ρ}$;
$l = \frac{144 * 0,2}{1,1} = 26,2$ м.
Ответ: 26,2 м.

Задание № 1173

Сварочный аппарат присоединяют к источнику тока медными проводами длиной 200 м и площадью поперечного сечения 500 $мм^{2}$. Каковы потери мощности в проводах, если сила тока в них 100 А?

Решение

Дано:
S = 500 $мм^{2}$;
I = 100 А;
$ρ = 0,017 \frac{Ом * мм^{2}}{м}$;
l = 200 м.
Найти:
P − ?
Решение:
Найдем сопротивление проводов:
$R = \frac{ρl}{S}$;
$R = \frac{0,017 * 200}{500} = 0,0068$ Ом;
Найдем мощность тока в проводах:
$U = IR$;
$P = UI = I^{2}R$;
$P = 100 ^{2} * 0,0068 = 68$ Вт.
Ответ: 68 Вт.